A rectangular coil of N-turns, area A is held in a uniform magnetic field B. If the coil is rotated at a steady angular velocity ω, deduce an expression for the induced emf in the coil at any instant of time.
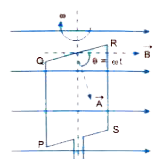
Consider a rectangular coil PQRS of N turns, each of area A, held in a uniform magnetic field →B. Let the coil be rotated at a steady angular velocity w about its own axis.
Let at any instant t, normal to the area (i.e., the area vector →A) subtends an angle θ=ωt from direction of magnetic field →B. Then, at that moment, the magnetic flux linked with the coil is
ϕB=N→B.→A=NBAcosθ=NBAcosωt
∴ Induced emf ɛ=−(dϕB)dt=−ddt(NBAcosωt)
=−NBAddt(cosωt)=NBAωt
where ɛ0=NBAω = maximum value of induced emf.
If the coil be rotating at .f. revolutions per second, then ω=2πf and the maximum induced emf
ɛ0=NBAω=2πfNBA
Topper's Solved these Questions
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Long Answer Questions -I
16 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Long Answer Questions -II
9 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Very Short Answer Questions
30 Videos
- ELECTROMAGNETIC WAVESBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SELF ASSESSMENT TEST (SECTION C)
1 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
Similar Questions
A coil of cross-sectional area A having n turns is placed in uniform magnetic field B. When it is rotated with an angular velocity ω, the maximum e.m.f. induced in the coil will be :
View SolutionIn the above question if the coil rotates with a constant angular velocity ω, the EMF induced in it
View Solution
Knowledge Check
A coil of cross-sectional area A having n turns is placed in uniform magnetic field B. When it is rotated with an angular velocity ω, the maximum e.m.f. induced in the coil will be :
A12 nBAωB32 nBAωC3 nBAωDnBAωA circular coil of radius r is placed in a uniform magnetic field B. The magnetic field is normal to the plane of the coil is rotated at an angular speed of ω, about its own axis , then the induced emf in the coil is __
 ABAω2πBB(2πr)ωC0Dnone of the above
ABAω2πBB(2πr)ωC0Dnone of the aboveA rectangular coil of single trun, having area A , rotates in a uniform magnetic field B with an angular velocity ω about an axis prependicular to the field. If initially the plane of the coil is perpendicular to the field, then the average induced emf when it has rotate through 90∘ is
AωBAπBωBA2πCωBA4πD2ωBA4π
A coil of metallic wire is held stationary in a non-uniform magnetic field. An emf is induced in the coil.
View SolutionState the working of a.c. generator with the help of a labelled diagram. The coil of an a.c. generator having N turns, each of area A, is rotated with a constant angular velocity ω. Deduce the expression for the alternating e.m.f. generated in the coil. What is the source of energy generation in this device?
View SolutionIn the above problem, if the coil rotates with a constant angular velocity ω, the emf induced in it
View SolutionA rectangular coil of area→Aand number of turns n is placed in a uniform magnetic field vecB. If the coil carries a current I, then the torque acting on the coil is given by
View SolutionA rectangular coil ABCD is rotated in uniform magnetic field with constant angular velocity about its one of the diameter as shown in figure. The induced emf will be maximum, when the plane of the coil is :-
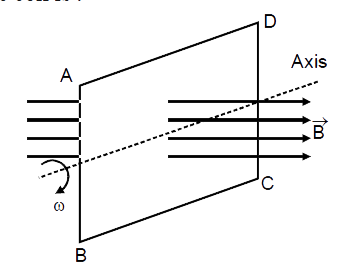
View Solution
