Two electrons are fixed at a seperation of 2d from each other.A proton is placed at the mid point and displaced slightly in a direction perpendicular to line joining the two electrons. Find frequency of oscillation of proton
f=12π(√2ke2md3)
f=12π(√ke2md3)
f=12π(√ke22md3)
none
To solve the problem, we need to analyze the forces acting on the proton placed at the midpoint between the two electrons and derive the frequency of oscillation when the proton is slightly displaced.
1. Understanding the Setup:
- We have two electrons fixed at a separation of 2d.
- A proton is placed at the midpoint, which is at a distance d from each electron.
2. Displacement of the Proton:
- Let the proton be displaced slightly in a direction perpendicular to the line joining the two electrons. Let this displacement be y.
3. Calculating the Forces:
- The force between the proton and each electron can be calculated using Coulomb's law:
F=k⋅e2d2
where k is Coulomb's constant, and e is the charge of an electron (and also the charge of the proton).
4. Components of Forces:
- When the proton is displaced by y, the distance from the proton to each electron becomes slightly more complicated. However, for small displacements, we can approximate the forces acting on the proton.
- The net force acting on the proton due to both electrons will have a vertical component that causes the proton to accelerate upwards.
5. Finding the Net Force:
- The net force Fnet acting on the proton can be expressed as:
Fnet=2F⋅sin(θ)
- For small angles, sin(θ)≈tan(θ)≈yd, so:
Fnet≈2F⋅yd
6. Substituting the Force:
- Substitute F into the equation:
Fnet≈2(k⋅e2d2)⋅yd=2k⋅e2d3⋅y
7. Relating to Acceleration:
- According to Newton's second law, F=m⋅a, where m is the mass of the proton and a is the acceleration:
m⋅a=−2k⋅e2d3⋅y
- This implies:
a=−2k⋅e2m⋅d3⋅y
8. Identifying Simple Harmonic Motion:
- The equation a=−ω2y indicates that the motion is simple harmonic, where:
ω2=2k⋅e2m⋅d3
9. Finding the Frequency:
- The angular frequency ω is related to the frequency f by:
ω=2πf
- Therefore, the frequency f can be expressed as:
f=12π√2k⋅e2m⋅d3
Final Answer:
f=12π√2k⋅e2m⋅d3
- We have two electrons fixed at a separation of 2d.
- A proton is placed at the midpoint, which is at a distance d from each electron.
- Let the proton be displaced slightly in a direction perpendicular to the line joining the two electrons. Let this displacement be y.
- The force between the proton and each electron can be calculated using Coulomb's law:
F=k⋅e2d2
where k is Coulomb's constant, and e is the charge of an electron (and also the charge of the proton).
- When the proton is displaced by y, the distance from the proton to each electron becomes slightly more complicated. However, for small displacements, we can approximate the forces acting on the proton.
- The net force acting on the proton due to both electrons will have a vertical component that causes the proton to accelerate upwards.
- The net force Fnet acting on the proton can be expressed as:
Fnet=2F⋅sin(θ)
- For small angles, sin(θ)≈tan(θ)≈yd, so:
Fnet≈2F⋅yd
- Substitute F into the equation:
Fnet≈2(k⋅e2d2)⋅yd=2k⋅e2d3⋅y
- According to Newton's second law, F=m⋅a, where m is the mass of the proton and a is the acceleration:
m⋅a=−2k⋅e2d3⋅y
- This implies:
a=−2k⋅e2m⋅d3⋅y
- The equation a=−ω2y indicates that the motion is simple harmonic, where:
ω2=2k⋅e2m⋅d3
- The angular frequency ω is related to the frequency f by:
ω=2πf
- Therefore, the frequency f can be expressed as:
f=12π√2k⋅e2m⋅d3
f=12π√2k⋅e2m⋅d3
Similar Questions
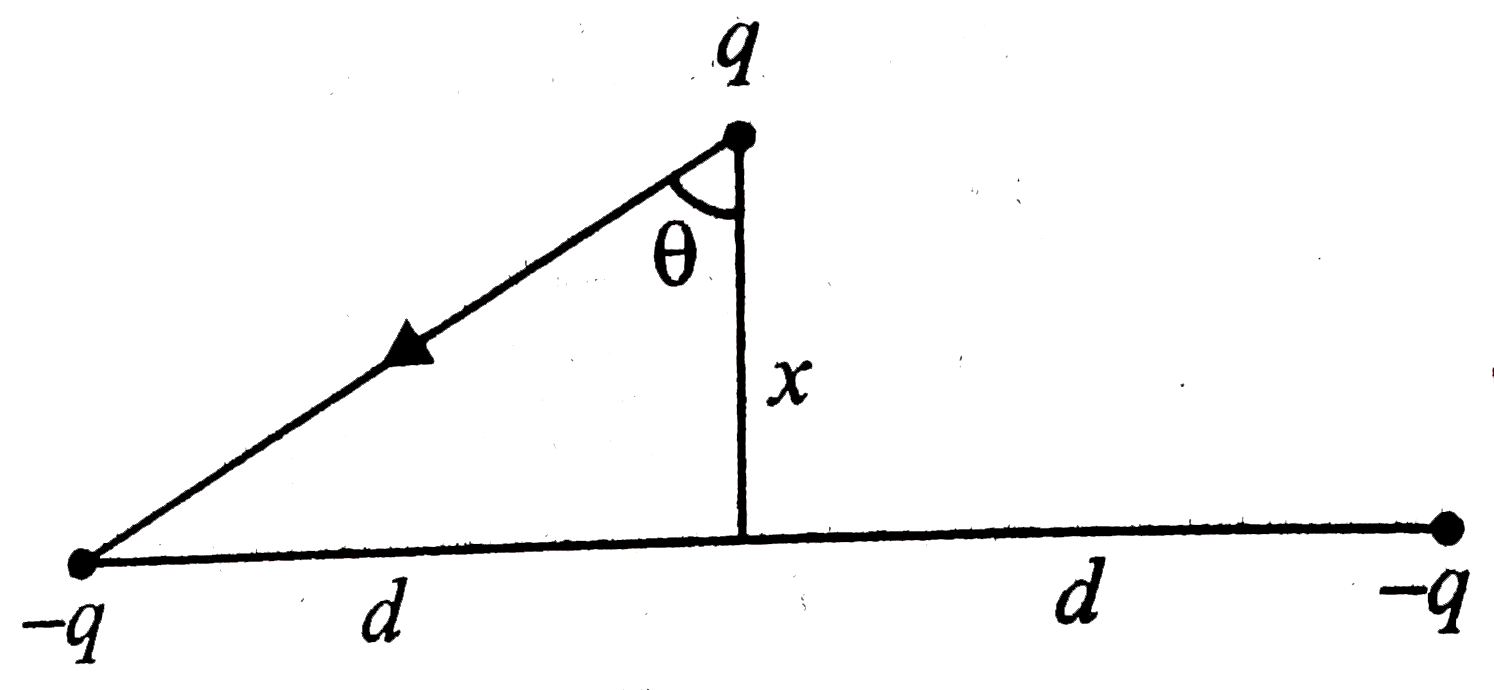
Two charges −q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced at the mid-point is placed slightly by x(x<<d) perpendicular to the line joining the two fixed charges as shown in Fig. Show that q will perform simple harmonic oscillarion of time period.
T=[8π3∈0md3q2]1/2
View SolutionTwo point charge Q and 4Q are fixed at a distance of 12cm from each other. Sketch lines of force and locate the neutral point, if any .
View Solution
Knowledge Check
Two electrons each are fixed at a distance '2d'. A third charge proton placed at the midpoint is displaced slightly by a distance x(x<<d) perpendicular to the line joining the two fixed charges. Proton will execute simple harmonic motion having angular frequency : (m = mass of charged particle)
A(2q2πε0md3)12B(πε0md32q2)12C(q22πε0md3)12D(2πε0md3q2)12Two parallel beams of protons and electrons, carrying equal currents are fixed at a separation d. The protons and electrons move in opposite directions. There is a point P on the straight perpendicular line joining the two beams at a distance x from one beam. The magnetic field at this point is B. If B is plotted against x, it can be represented by the curve.
A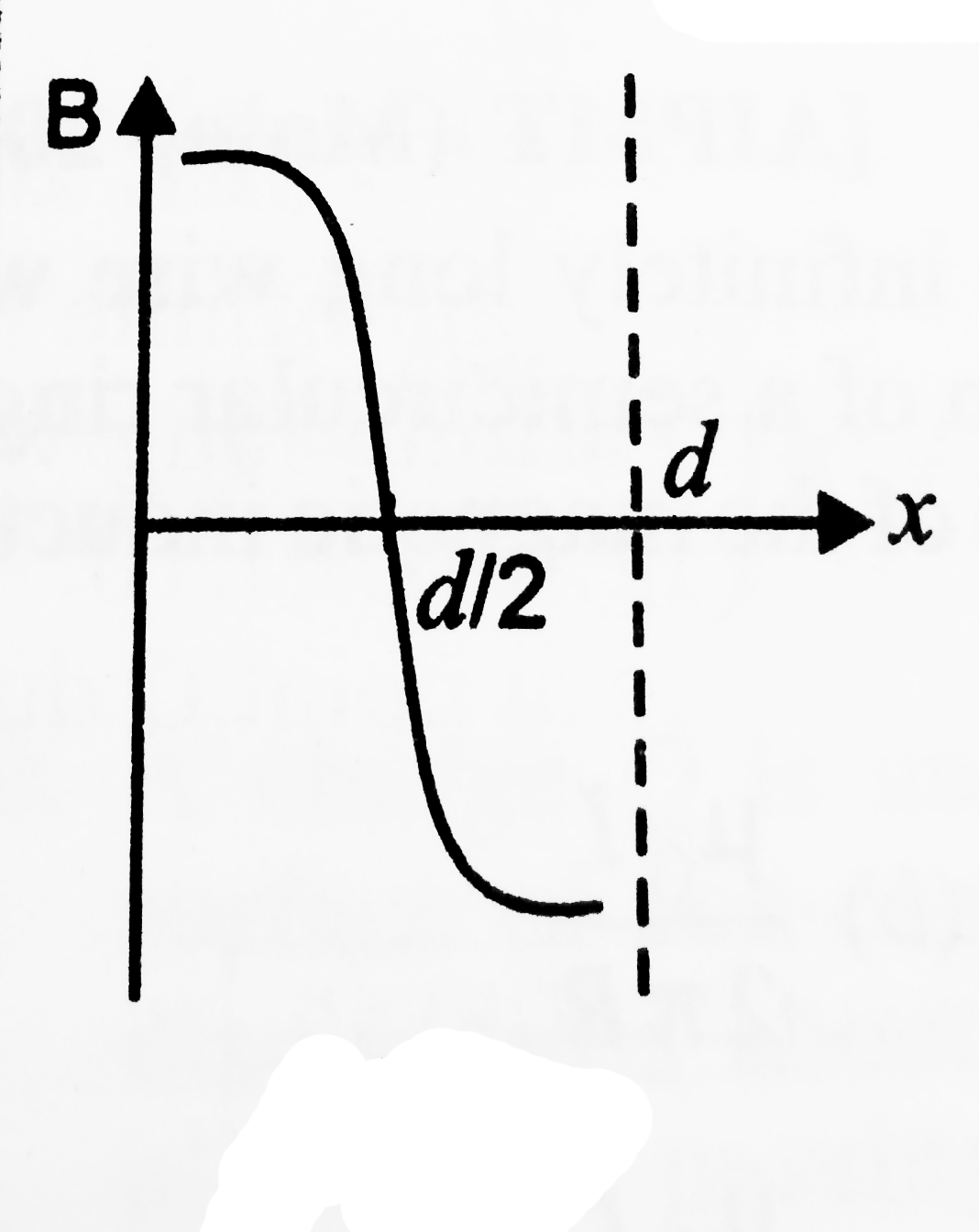 B
B C
C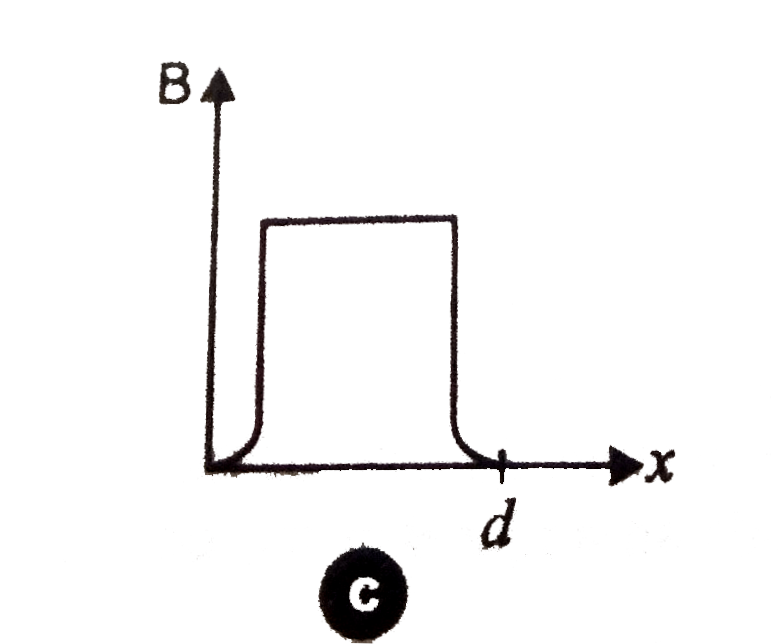 D
D
Find the odd statement : Two lines are perpendicular to each other if they are,
AAdjacent sides of a rectangle.BDiagnoals of a rhombus.CHypotenuse and one side of a right-angle triangle.DAdjacent sides of a square.
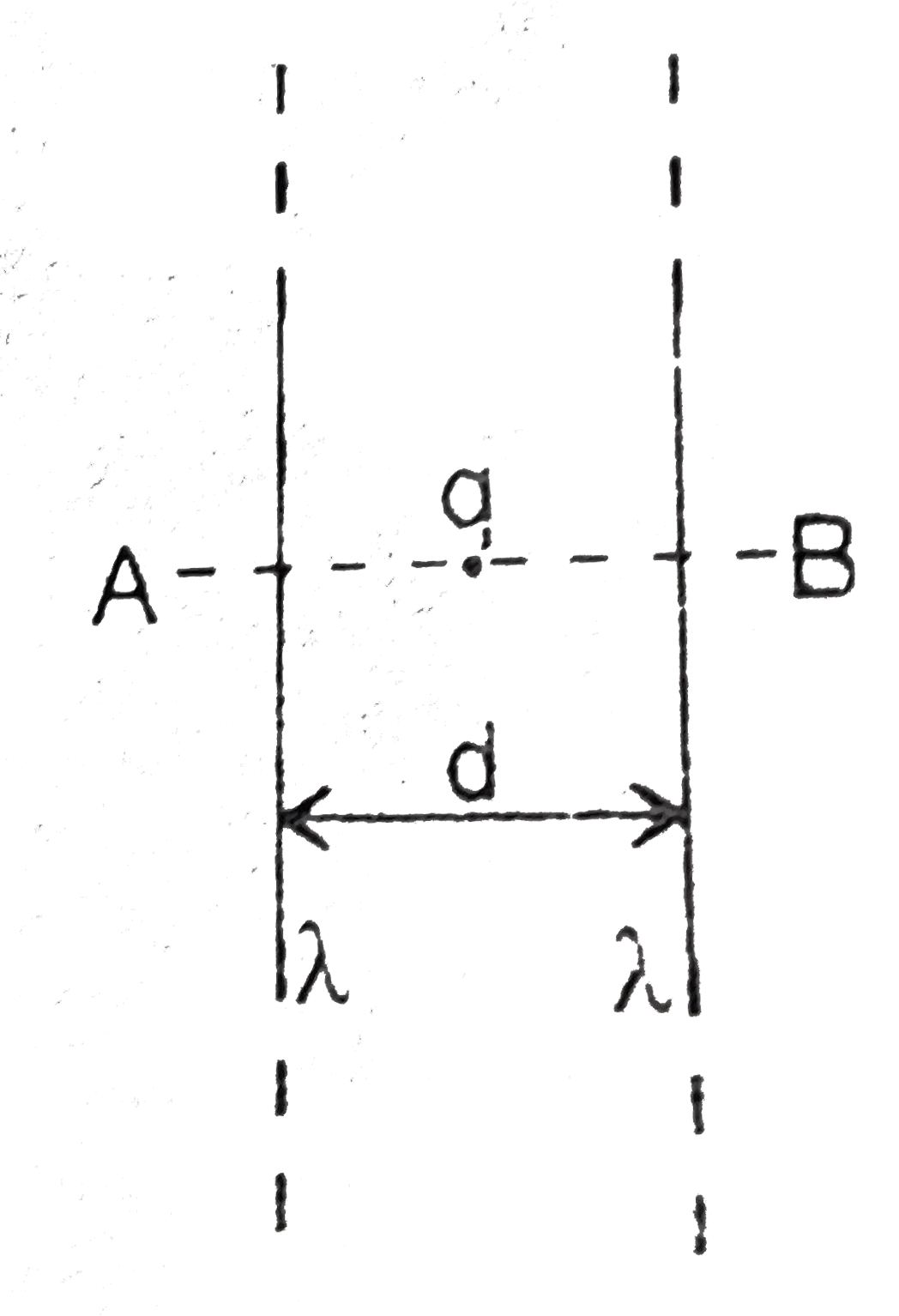
Two infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
View SolutionThe two coherent sources of monochromatic light of wavelength λ are located at a separation λ. The two sources are placed on a horizontal line and screen is placed perpendicular to the line joining the sources. Find position of the farthest minima from the centre of the sources.
View SolutionTwo points charges , each Q , are fixed at separation 2d. A charged particle having charge q and mass m is placed between them.
(a) Now this charged particle is slightly displaced along the line joining the charges , slow that it will execute simple harmonic motion and find the time period of oscillation.
(b) If charge q is negative and it is displaced slightly perpendicular to the line joining the charges , repeat the part (a).
View SolutionTwo protons are a distance of 1×10−10cm from each other. The force acting on them are
View SolutionTwo masses of mass m each are fixed at a separation distance of 2d. A small mass ms placed midway, when displaced slightly, starts oscillating. Then :
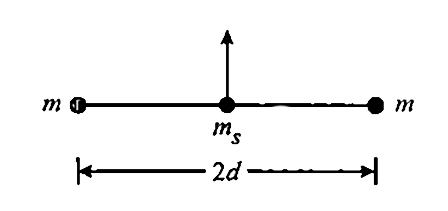
View Solution
