Consider the function f(x)=3x4−8x3+12x2−48x+25
Find the turning point of f(x).Solution in Malayalam
Step by step video & image solution for Consider the function f(x)=3x^4-8x^3+12x^2-48x+25 Find the turning point of f(x). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
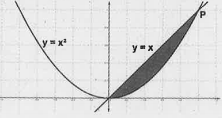
Consider the following figure
find the point of intersection (P) of the parabola and the line.
View SolutionFind the absolute maximum and absolute minimum values of f(x)=3x4−8x3+12x2−48x+25 in [0, 3]
View Solutionconsider the function f(X) =3x4+4x3−12x2
The range of the function y=f(x) is
View Solutionप्रदत अंतराल में निम्नलिखित फलनों के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए|
f(x)=3x4−8x3+12x2−48x+25(in)[0,3] में|
View SolutionThe minimum value of function f(x)=3x4−8x3+12x2−48x+25 on [0,3] is equal to
View Solutionf(x)=3x4−8x3+12x2−48x+25,[0,3] फलन का दिया गया अन्तराल में निरपेक्ष उच्चिष्ठ और निरपेक्ष निम्निष्ठ मान ज्ञात कीजिए
View Solutionf(x)=3x4−8x3+12x2−48x+1,[1,4] फलन का दिया गया अन्तराल में निरपेक्ष उच्चिष्ठ और निरपेक्ष निम्निष्ठ मान ज्ञात कीजिए
View Solutionअंतराल [0,3] में फलन f(x)=3x4−8x3+12x2−48x+7 के उच्चिष्ठ और निम्निष्ठ मान ज्ञात करें |
View SolutionFind both the maximum value and the minimum value 3x4−8x3+12x2−48x+25 on the interval [0,3].
View Solutionअंतराल [1,3] में फलन 3x4−8x3+12x2−48x+25 के लिए उच्च्ष्ठि व निम्निष्ठ मान क्रमशः है
View Solutionconsider the function f(X) =3x4+4x3−12x2
The range of the function y=f(x) is
View SolutionFind both the maximum value and the minimum value of f(x)=3x4−8x3+12x2−48x+25 on the interval [0, 3].
View SolutionConsider the function f(x)=3x4−8x3+12x2−48x+25
Explain the nature of the turning points.
View SolutionConsider the function f(x)=3x4−8x3+12x2−48x+25
Find the absolute extreme values of f(x).x∈[0,3] are respectively
View SolutionThe minimum value of function f(x)=3x4−8x3+12x2−48x+25 on [0,3] is equal to...a)25 b)−39 c)−25 d)39
View Solution
