The linear momentum of a particle varies with time as . Which of the following graph represents force and time relation ?
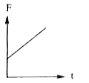
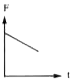
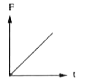
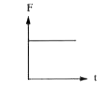
The correct Answer is:A
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II136videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - KINETIC THEORY OF GASESEXERCISE - Practice Exercise15videos
KINETIC THEORY OF GASES
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-343videos
MECHANICAL PROPERTIES OF FLUIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
The linear momentum of a particle varies with time t as p=a+bt+ct2. Then, whichh of the following is correct?
AVelocity of particle is inversely proportional to timeBDisplacement of the particle is independent of timeCForces varies with time in a quadratic mannerDForce is independent linearly on time - Question 2 - Select One
The linear momentum P of a particle varies with time as follows P=a+bt2
Where a and b are constants. The net force acting on the particle isAproportional to tBproportional to t2CZeroDconstant - Question 3 - Select One
The force acting on a particle moving along a straight line varies with time as shown in diagram.
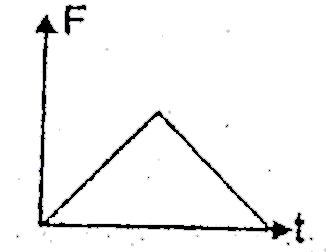
Which of the following graphs is best representative of its speed and time graphs. Initial velocity the particle is zero.A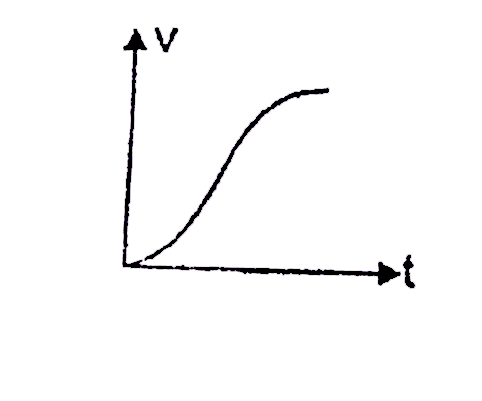
B
C
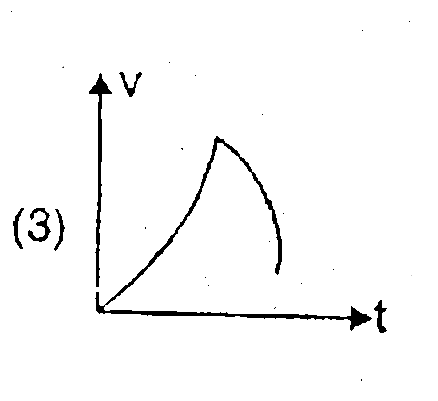D
The linear momentum P of a particle varies with time as follows P=a+bt2
Where a and b are constants. The net force acting on the particle isView SolutionThe force acting on a particle moving along a straight line varies with time as shown in diagram.
Which of the following graphs is best representative of its speed and time graphs. Initial velocity the particle is zero.View SolutionThe force acting on a particle moving along a straight line varies with time as shown in diagram.
Which of the following graphs is best representative of its speed and time graphs. Initial velocity the particle is zero.View SolutionThe position x of a particle varies with time t as x=at^(2)-bt^(3) .The acceleration of the particle will be zero at time t equal to
View SolutionThe position x of a particle varies with time t as x=at2−bt3. The acceleration at time t of the particle will be equal to zero, where (t) is equal to .
View Solution