A ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface and rebounds from it at an angle β with the surface. Then :
(θ+β) is equal to 90∘ is wall is smooth
If wall is smooth coefficient of resitution =tanβcotθ
If wall if smooth coefficient of resitution <tanβtanθ
None of these
The correct Answer is:B
Similar Questions
A ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface. and rebounds from it at an angle β with the surface. Then
View SolutionA ball strikes a smooth horizontal floor at an angle α with the normal to the surface and after rebounding from the floor , ball moves at an angle β with the normal . Find the relation between α and β if coefficient of elasticity is e .
View Solution
Knowledge Check
A ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface. and rebounds from it at an angle β with the surface. Then
A(θ+β)<90∘ if the wall is smoothBif the wall is rough , coefficient of restitution =tanβ/cosθCif the wall is rough, coefficient of restition
<tanβ/cotθDnone of theseA ball is projected at t=0 with velocity v0 at angle θ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
ABall will return to ground at t=2v0sinθgBd=e(R−L)(whereRisv0sin2θg)Cmaximum height during motion =v20sin2θ2gDit will return to ground at t<2v0sinθg
A ball of mass 600 gm strikes a wall with a velocity of 5ms−1 at an angle 30∘ with the wall and rebounds with the same speed at the same angle with the wall. The change in momentum of the ball is, (in kg ms−1)
View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionA 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
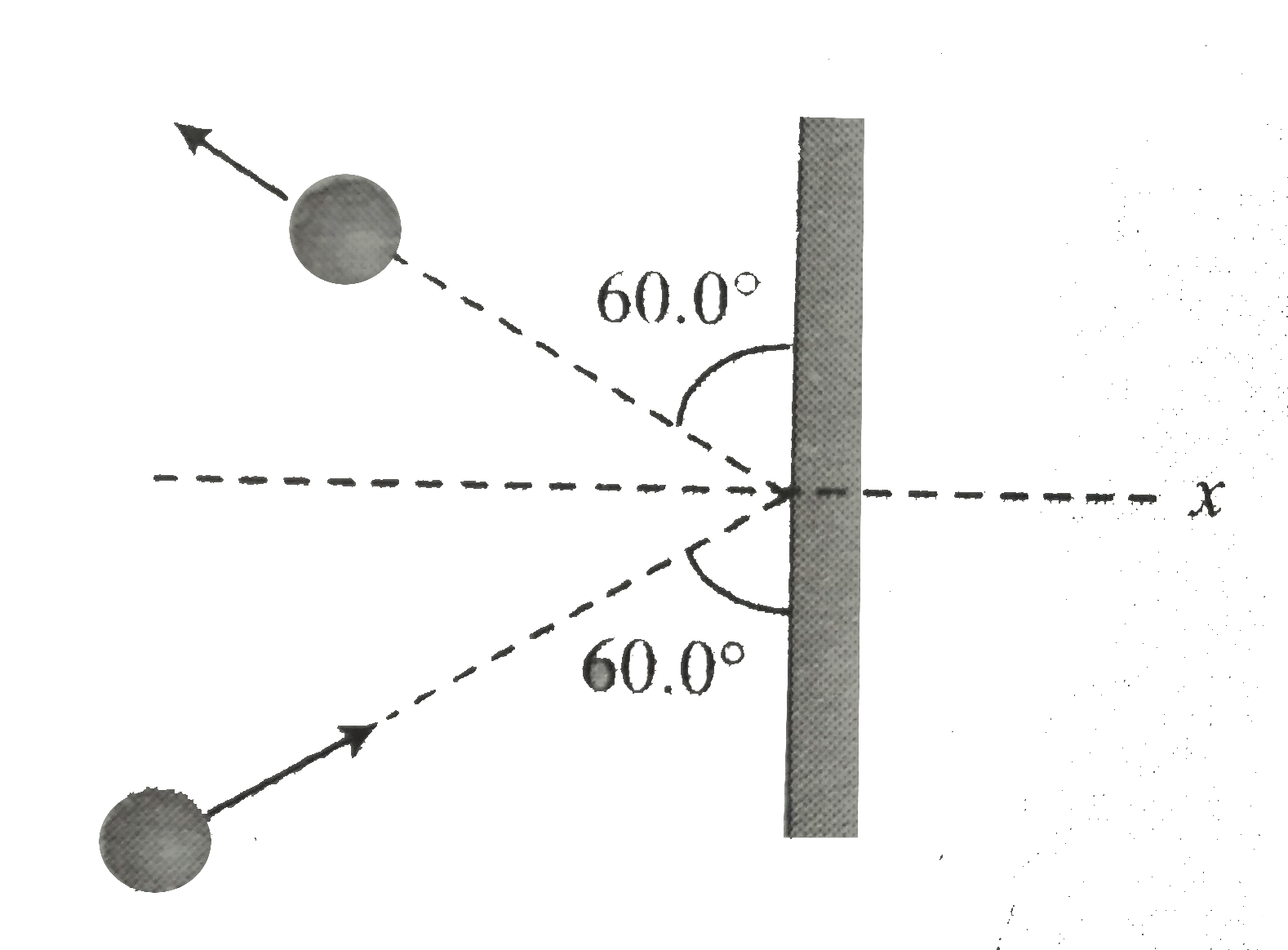
View SolutionA 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.

View SolutionA ball is projected at t=0 with velocity v0 at angle θ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
View Solution
