प्रकथन-1 : तल x−y+z=5 में बिन्दु B(1, 3, 4) का दर्पण प्रतिबिम्ब बिन्दु A(3, 1, 6) है।
प्रकथन-2 : तल x-y+z= 5, A(3, 1, 6) तथा B(1, 3, 4) को मिलाने वाले रेखाखण्ड को समद्विभाजित करता है।
कथन-1 सही है, कथन-2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही है
कथन-1 सही है, कथन-2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही नहीं है।
कथन-1 सही है, कथन-2 गलत है
कथन-1 गलत है, कथन-2 सही है
The correct Answer is:B
Step by step video, text & image solution for प्रकथन-1 : तल x -y+z = 5 में बिन्दु B(1, 3, 4) का दर्पण प्रतिबिम्ब बिन्दु A(3, 1, 6) है। प्रकथन-2 : तल x-y+z= 5, A(3, 1, 6) तथा B(1, 3, 4) को मिलाने वाले रेखाखण्ड को समद्विभाजित करता है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (COMPREHENSION TYPE QUESTIONS) (PASSAGE-I)
3 Videos
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (COMPREHENSION TYPE QUESTIONS) (PASSAGE-II)
3 Videos
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (MORE THAN ONE CORRECT ANSWERS)
10 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)
5 Videos
- द्विपद प्रमेय तथा गणितीय आगमन BOOK - ERRORLESS HINDICHAPTER - द्विपद प्रमेय तथा गणितीय आगमन EXERCISE - JEE Advanced (Matrix Math type questions)
5 Videos
Similar Questions
माना कि a,b,c ऐसी तीन वास्तविक संख्यायों हैं जो
[abc]⎡⎢⎣197827737⎤⎥⎦=[000] को संतुष्ट करती हैं।
यदि समीकरण E के संदर्भ में बिंदु P(a,b,c) समतल 2x+y+z=1 पर स्थित है तो 7a+b+c का मान है
View Solutionमाना कि रेखाएं निम्न हैं L1:x+13=y+21=z+12:L2x−21=y+22=z−33
इकाई सदिश जो L1 तथा L2 दोनों के लम्बवत् होगा
View Solutionएक रेखा l जो मूलबिंदु से गुजरती है रेखाओं
l1:(3+t)ˆi+(−1+2t)ˆj+(4+2t)ˆk,−∞<t<∞
l2:(3+2s)ˆi+(3+2s)ˆj+(2+s)ˆk,−∞<s<∞
पर लम्बवत है। तब l2 पर स्थित बिंदु (बिंदुओं) के निर्देशांक जो रेखाओं l तथा l1 के प्रतिच्छेद बिंदु से √17 की दूरी पर है निम्न है: (i) (73,73,53) (ii) (−1,−1,0)
(iii) (1,1,1) (iv) (79,79,89)
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
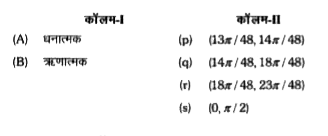
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये

View Solutionनिम्न रेखायुग्मों के बीच का कोण ज्ञात कीजिए-
(i)x+33=y−15=z+34 तथा x+11=y−41=z−52
(ii) x+11=y−41=z−52 तथा x+33=y−22=z+2−1
(iii) x−32=y+51=1−z3 तथा x3=y−12=z+2−1
(iv) x−42=y−15=z+3−3 तथा x+2−1=y−48=z−54
(v) x−43=y+14=z−65 तथा x−51=2y+5−1=z−31
(vi) 5−x3=y+3−4,z=7 तथा x1=1−y2=z−62
(vii)x+11=2y−33,z−62 तथा x−43=y+3−2,z=5
View Solutionनिम्न रेखायुग्मों के बीच की न्यूतम दुरी ज्ञात कीजिए-
(i) x−3−1=y−42=z+21 तथा x−11=y+73=z+22
(ii)x+17=y+1−6=z−52 तथा x−31=y−5−2=z−71
(iii) x+2−9=y−14=z−52 तथा x−23−6=y−19−4=z−253
View SolutionThe lines x−12=y−24=z−36 and x−14=y−25=z−37 are
View Solutionनिम्नलिखित रेखा युग्मों के बीच का कोण ज्ञात कीजिये
x+33=y−15=z+34 और x+11=y−41=z−52
View Solutionयदि ज्यामिति आरेख पर बिन्दु P सम्मिश्र संख्या z=x+iy को निरूपित करता है , तो P का बिन्दुपथ ज्ञात कीजिए जबकि
(a)|z−1|=|z−3| (b)|z−1|=5|z+1| (c)arg(z−3)=π3
View Solutionस्तम्भ(A)स्तम्भ(B)(1) बिन्दु (3,4) की मूल बिन्दु से दुरी होगी (a)37(2)यदि बिन्दु (3,5) ,(6,9) तथा (x,3) संरेख हो, तो का x मान होगा: (b)3(3)बिंदुओं (3,5) तथा (-4,2) को मिलाने वाली रेखा की प्रवणता होगी :(b)72(4)kके किस मान के लिए रेखाएँ y=x+1,y=2+3 तथा संगामी होंगी?(c)5(5)रेखा की x+sqrt(3)y+7=0 मुलबिन्दु से लाम्बिक दुरी होगी (d)4
View Solutionसिध्द कीजिए कि बिन्दु z का बिन्दुपथ जो प्रतिबन्ध argz−1z+1=π3 को संतुष्ट करता है, होगा - x2+y2−2√3y−1=0
View Solutionवह समतल, जो बिन्दुओ (−3,−3,4) तथा (3,7,6) को मिलाने वाले रेखाखण्ड का लंबसमद्विभाजक करता है, निम्न में से किस एक बिंदु से होकर जाता है?
View Solutionदो रेखाएं x−31=y+13=z−6−1 तथा x+57=y−2−6=z−34 बिन्दु R पर काटती है । बिन्दु R के XY तल के प्रतिबिम्ब के निर्देशांक है
View Solutionदो रेखाओ x+23=y−25=z+57 तथा x−11=y−44=z+47 को अंतर्विष्ट करने वाले समतल कि मूलबिंदु से लंबवत दुरी है
View Solutionदीर्घवृत्त x236+y29=1 की जीवा का समीकरण, जोकि बिन्दु (2, 1) से जाती है, तथा यह बिन्दु जीवा को दो बराबर-बराबर भागों में विभाजित करता है, होगा
View Solution
