वक्तव्य I - रेखाएँ x−11=y−1=z+11 और x+21=y+12=z3 समतलीय है और समतल 5x+2y−3z−8=0 में है।
वक्तव्य II - रेखा x−21=y+12=z3 समतल 3x+6y+9z−8=0 पर लम्ब है और समतल x+y−z=0 के समान्तर है।
कथन-1 सही है, कथन-2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही है
कथन-1 सही है, कथन-2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही नहीं है।
कथन-1 सही है, कथन-2 गलत है
कथन-1 गलत है, कथन-2 सही है
Step by step video, text & image solution for वक्तव्य I - रेखाएँ (x-1)/(1)=(y)/(-1)=(z+1)/(1) और (x+2)/(1)=(y+1)/(2)=(z)/(3) समतलीय है और समतल 5x+2y-3z-8=0 में है। वक्तव्य II - रेखा (x-2)/(1)=(y+1)/(2)=(z)/(3) समतल 3x+6y+9z-8=0 पर लम्ब है और समतल x+y-z=0 के समान्तर है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (COMPREHENSION TYPE QUESTIONS) (PASSAGE-I)3videos
त्रिविमीय निर्देशांक ज्यामिति
- BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (COMPREHENSION TYPE QUESTIONS) (PASSAGE-II)3videos
त्रिविमीय निर्देशांक ज्यामिति
- BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (MORE THAN ONE CORRECT ANSWERS)10videos
त्रिविमीय निर्देशांक ज्यामिति
- BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)5videos
त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकाये
- BOOK - ERRORLESS HINDICHAPTER - द्विपद प्रमेय तथा गणितीय आगमन EXERCISE - JEE Advanced (Matrix Math type questions)5videos
द्विपद प्रमेय तथा गणितीय आगमन
Similar Questions
माना कि a,b,c ऐसी तीन वास्तविक संख्यायों हैं जो
[abc]⎡⎢⎣197827737⎤⎥⎦=[000] को संतुष्ट करती हैं।
यदि समीकरण E के संदर्भ में बिंदु P(a,b,c) समतल 2x+y+z=1 पर स्थित है तो 7a+b+c का मान है01:20View Solutionमाना कि रेखाएं निम्न हैं L1:x+13=y+21=z+12:L2x−21=y+22=z−33
इकाई सदिश जो L1 तथा L2 दोनों के लम्बवत् होगा01:32View Solutionएक रेखा l जो मूलबिंदु से गुजरती है रेखाओं
l1:(3+t)ˆi+(−1+2t)ˆj+(4+2t)ˆk,−∞<t<∞
l2:(3+2s)ˆi+(3+2s)ˆj+(2+s)ˆk,−∞<s<∞
पर लम्बवत है। तब l2 पर स्थित बिंदु (बिंदुओं) के निर्देशांक जो रेखाओं l तथा l1 के प्रतिच्छेद बिंदु से √17 की दूरी पर है निम्न है: (i) (73,73,53) (ii) (−1,−1,0)
(iii) (1,1,1) (iv) (79,79,89)15:15View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
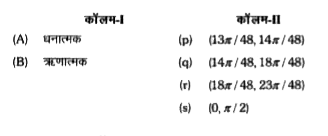 06:50View Solution
06:50View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
 03:53View Solution
03:53View SolutionIf x(2x+y+z)=y(x+2y+z)=z(x+y+2z)=a , then find a if x+y+z≠0 . (a)13 (b) 14 (c) 12 (d) 18
03:33View Solution(2-3x)/(x)+(2-3y)/(y)+(2-3z)/(z)=0 then (1)/(x)+(1)/(y)+(1)/(z)=
04:10View SolutionStatement 1: The lines x−11=y−1=z+11 and x−22=y+12=z3 are coplanar and the equation of the plnae containing them is 5x+2y−3z−8=0
Statement 2: The line x−21=y+12=z3 is perpendicular to the plane 3x+5y+9z−8=0 and parallel to the plane x+y−z=001:44View Solution1/x−1y+1z=4,2x+1y−3z=0,1x+1y+1z=2(x,y,z≠0)
03:12View Solutionसिद्ध कीजिए कि रेखाएँ x+32=y+53=z−7−3 और x+14=y+15=z+1−1 समतलीय है।
03:25View Solutionसरल रेखाएँ x−21=y−31=z−4−k और x−1k=y−42=z−51 समतलीय होंगे यदि k =
03:04View Solutionउस रेखा के समीकरण ज्ञात कीजिए जो बिंदु (−1,3,2) से होकर जाती है तथा रेखाओं x1=y2=z3 और x+2−3=y−12=z+15 पर लम्ब है।
03:52View Solutionउस समतल का समीकरण ज्ञात कीजिए जो X, Y और Z-अक्षों पर क्रमशः 1, 2 और 3 अन्तःखण्ड काटता है |
04:22View Solutionc और d के मान ज्ञात कीजिए यदि समतल 2x+4y−cz+d=0 में सरल रेखा x−12=y−31=z−14 स्थित है।
04:55View Solutionयदि रेखा x−32=y−43=z−54 समतल 4x+4y−kz−d=0 पर स्थित है तो k और d के मान है -
02:28View Solutionरेखा x−23=y+1−1=z−32 और समतल 3x+4y+z+5=0 के मध्य कोण ज्ञात कीजिए।
10:13View Solution

