कथन-1: यदि A,B,C क्रमशःYZ, ZX तथाXY समतल में बिन्दु Pa,b,c) के प्रतिबिम्ब हो, तो उस समतल का समीकरण जो बिन्दुओं A,B,C से होकर गुजरता हो तथा निर्देशांक अक्षों से क्रमशः, a,b,c अंतः खण्ड काटता हो।
कथन-2 : बिन्दु (x1,y1,z1) का प्रतिबिम्ब (α,β,γ) समतल ax+by+cz+d=0 में α−x1a=β−y1b=γ−z1c=2(ax1+by1+cz1+d)a2+b2+c2 के दारा दिया जाता है।
कथन-1 सही है, कथन-2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही है
कथन-1 सही है, कथन-2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही नहीं है।
कथन-1 सही है, कथन-2 गलत है
कथन-1 गलत है, कथन-2 सही है
The correct Answer is:A
Topper's Solved these Questions
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (COMPREHENSION TYPE QUESTIONS) (PASSAGE-I)
3 Videos
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (COMPREHENSION TYPE QUESTIONS) (PASSAGE-II)
3 Videos
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (MORE THAN ONE CORRECT ANSWERS)
10 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)
5 Videos
- द्विपद प्रमेय तथा गणितीय आगमन BOOK - ERRORLESS HINDICHAPTER - द्विपद प्रमेय तथा गणितीय आगमन EXERCISE - JEE Advanced (Matrix Math type questions)
5 Videos
Similar Questions
माना कि a,b,c ऐसी तीन वास्तविक संख्यायों हैं जो
[abc]⎡⎢⎣197827737⎤⎥⎦=[000] को संतुष्ट करती हैं।
यदि समीकरण E के संदर्भ में बिंदु P(a,b,c) समतल 2x+y+z=1 पर स्थित है तो 7a+b+c का मान है
View Solutionमाना कि रेखाएं निम्न हैं L1:x+13=y+21=z+12:L2x−21=y+22=z−33
इकाई सदिश जो L1 तथा L2 दोनों के लम्बवत् होगा
View Solutionएक रेखा l जो मूलबिंदु से गुजरती है रेखाओं
l1:(3+t)ˆi+(−1+2t)ˆj+(4+2t)ˆk,−∞<t<∞
l2:(3+2s)ˆi+(3+2s)ˆj+(2+s)ˆk,−∞<s<∞
पर लम्बवत है। तब l2 पर स्थित बिंदु (बिंदुओं) के निर्देशांक जो रेखाओं l तथा l1 के प्रतिच्छेद बिंदु से √17 की दूरी पर है निम्न है: (i) (73,73,53) (ii) (−1,−1,0)
(iii) (1,1,1) (iv) (79,79,89)
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
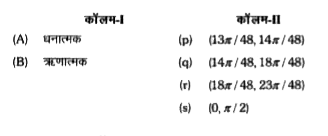
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये

View SolutionShow that the plane ax+by+cz+d=0 divides the line joining the points (x1,y1,z1)and(x2,y2,z2) in the ratio ax1+by1+cz1+dax2+by2+cz2+d .
View SolutionIf ax12+by12+cz12=ax22+by22+cz22=ax32+by32+cz32=d,ax23+by2y3+cz2z3=ax3x1+by3y1+cz3z1=ax1x2+by1y2+cz1z2=f, then prove that |x1y1z1x2y2z2x3y3z3|=(d−f){(d+2f)abc}1/2
View SolutionA=[[2,0,00,2,00,0,2]] and B=[[x_(1),y_(1),z_(1)x_(2),y_(2),z_(2)x_(3),y_(3),z_(3)]]
View SolutionIf Q(h,k) is the image of the point P(x_(1),y_(1)) w.r.to the straight line ax+by+c=0 then prove that (h-x_(1)):a=(k-y_(1)):b=-2(ax_(1)+by_(1)+c):a^(2)+b^(2) or (h-x_(1))/(a)=(k-y_(1))/(b)=(-2(ax_(1)+by_(1)+c))/(a^(2)+b^(2)) and find the image of (1,-2) w.r.t the straight line 2x-3y+5=0
View SolutionStatement 1: Let A,B,C be the image of point P(a,b,c) in YZ,ZX andXY planes respectively. Then, the equation of the plane passing through points A,B,C cuts intercepts a,b,c on the coordinate axes. Statement 2: The image (α,β,γ) of a point (x1,y1,z1) in the plane ax+by+cz+d=0 is given by α−x1a=β−y1b=γ−z1c=−2(ax1+by1+cz1+d)a2+b2+c2
View SolutionIf (x1,x2)2+(y1−y2)2=a2,(x2−x3)2+(y2−y3)2=b2(x3−x1)2+(y3−y1)2=c2. where a,b,c are positive then prove that 4∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣=(a+b+c)(b+c−a)<br>(c+a−b)(a+b−c)
View SolutionLet a=xˆi+12ˆj−ˆk,b=2ˆi+2xˆjj+ˆkandc=ˆi+ˆk. If b,c,a in that order form a left handed system, then find the value of x.
[x1a+y1b+z1c,x2a+y2b+z2c,x3a+y3b+z3c]
=∣∣ ∣ ∣∣x1y1z1x2y2z2x3y3z3∣∣ ∣ ∣∣[abc].
View SolutionIf (x1−x2)2+(y1−y2)2=a2,(x2−x3)2+(y2−y3)2=b2,(x3−x1)2(y3−y1)2=c2 and ∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣2=(a+b+c)(b+c−a)(c+a−b)(a+b−c) then the value of λ is:
View Solutionसिद्ध कीजिए कि समतल ax+by+cz+d=0 बिंदुओं (x1,y1,z1) और (x2,y2,z2) को मिलाने वाली रेखा को −ax1+by1+cz1+dax2+by2+cz2+d:1 के अनुपात में विभाजित करता है।
View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
View Solution
