A rod of length L is placed along the x-axis with one of its ends at the origin O. The mass of the rod increases linearly as dmdx=λx where λ is a constant

The position of the centre of mass C of the rod conincides with the geometrical centre C of the rod.
The moment of inertia of rod about y-axis is λL44
The moment of inertia about the perpendicular centroidal is 136λL4 axis.
All the above statement ar are wrong.
The correct Answer is:B, C
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - I) Moment of Inertia (Linked Comprehension Type questions)
3 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - I) Moment of Inertia (Matrix Matching Type Questions)
1 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - I) Moment of Inertia (Straight Objective Type Questions )
10 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
A non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
View SolutionA non-uniform thin rod of length L is palced along X-axis so that one of its ends is at the origin. The linear mass density of rod is λ=λ0x. The centre of mass of rod divides the length of the rod in the ratio:
View Solution
Knowledge Check
A non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
AL/2B2L/3CL/4DL/5A rod length L and mass M is placed along the x-axis with one end at the origin, as shown in the figure above. The rod has linear mass density λ=2ML2x, where x is the distance from the origin. Which of the following gives the x-coordinate of the rod's center of mass?
 A23LB14LC13LD12L
A23LB14LC13LD12LA rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density λ=ax, a being a positive constant. The electric potential at the point P (origin) as shown in the figure is
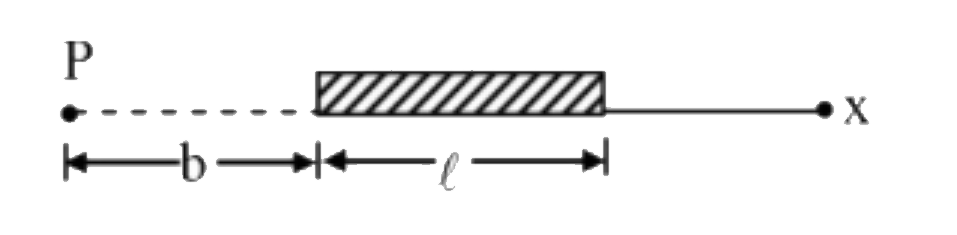 AV=a4πε0(lb(b+l))BV=a4πε0(bl(b+l))CV=a4πε0(bl)DV=a4πε0(lb)
AV=a4πε0(lb(b+l))BV=a4πε0(bl(b+l))CV=a4πε0(bl)DV=a4πε0(lb)
A rod length L and mass M is placed along the x-axis with one end at the origin, as shown in the figure above. The rod has linear mass density λ=2ML2x, where x is the distance from the origin. Which of the following gives the x-coordinate of the rod's center of mass?

View SolutionA rod of length L lies along the x-axis with its left end at the origin. It has a non-uniform charge density λ=αx, where a is a positive constant.
(a) What are the units of α?
(b) Calculate the electric potential at point A where x=−d .
View SolutionA rod of length L lies along the x-axis with its left end at the origin. It has a non-uniform charge density λ=αx, where a is a positive constant.
(a) What are the units of α?
(b) Calculate the electric potential at point A where x=−d .
View SolutionA rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density λ=ax, a being a positive constant. The electric potential at the point P (origin) as shown in the figure is

View SolutionA rod of length 'l' is placed along x-axis. One of its ends is at the origin. The rod has a non-uniform charge density λ= a, a being a positive constant. Electric potential at P as shown in the figure is -
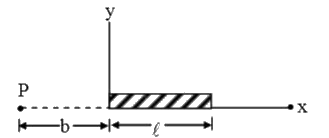
View Solution
