From a uniform disc of mass M and radius R, a concentric disc of radius $R / 2$ is cut out for the remaining abgular disc $I_{1}$ is the moment of inertia about axis '1', $I_{2}$ about 2, $I_{3}$ about '3' and $I_{4}$ about '4' Axes '1' and '2' are perpendicular to the disc and '3' and '4' are in the plane of disc Axes '2', '3' and '4' intersect at a common point.

Text Solution

Verified by Experts

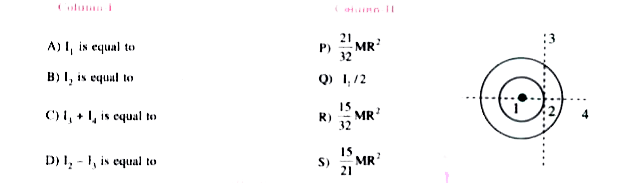
The correct Answer is:A-R; B-P; C-P; D-Q

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Out of a disc of mass M and radius R a concentric disc of mass m and radius r is removed. The M.I. of the remaining part about the symmetric axis will be :
A $(M - m) {(R + r)}^{2} / 2$
B $(M - m) (R^{2} - r^{2}) / 2$
C $(M - m) {(R - r)}^{2} / 2$
D $(M - m) (R^{2} + r^{2}) / 2$
Question 2 - Select One
A thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -

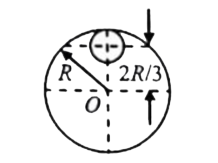A $4 M R^{2}$
B $9 M R^{2}$
C $\frac{37}{9} M R^{2}$
D $\frac{40}{9} M R^{2}$
Question 3 - Select One
The diagram shows a uniform disc of mass $M$ & radius ' $a$ ', if the moment of inertia of the disc about the axis $X Y$ is $I$ , its moment of inertia about an axis through $O$ and perpendicular to the plane of the disc is

A $\frac{4}{3} M a^{2}$
B $I + \frac{1}{4} M a^{2}$
C2I
D $\frac{I}{2}$

AAKASH SERIES-ROTATIONAL DYNAMICS -LECTURE SHEET (EXERCISE - I) Moment of Inertia (Matrix Matching Type Questions)

From a uniform disc of mass M and radius R, a concentric disc of radiu...
Text Solution

Home
Ask Doubt
Profile