A disc of mass radius R lies in the x-y plane with its centre at a distance a from the origin on the x-axis. Which of the following statements are correct ?
M.I. of the disc about x-axis MR2/4
M.I. of the disc about y-axis is M(R22+a2)
M.I. of the disc about z-axis is M(R22+a2)
All of the above
The correct Answer is:A, C
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - I) Moment of Inertia (Linked Comprehension Type questions)
3 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - I) Moment of Inertia (Matrix Matching Type Questions)
1 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - I) Moment of Inertia (Straight Objective Type Questions )
10 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
A uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
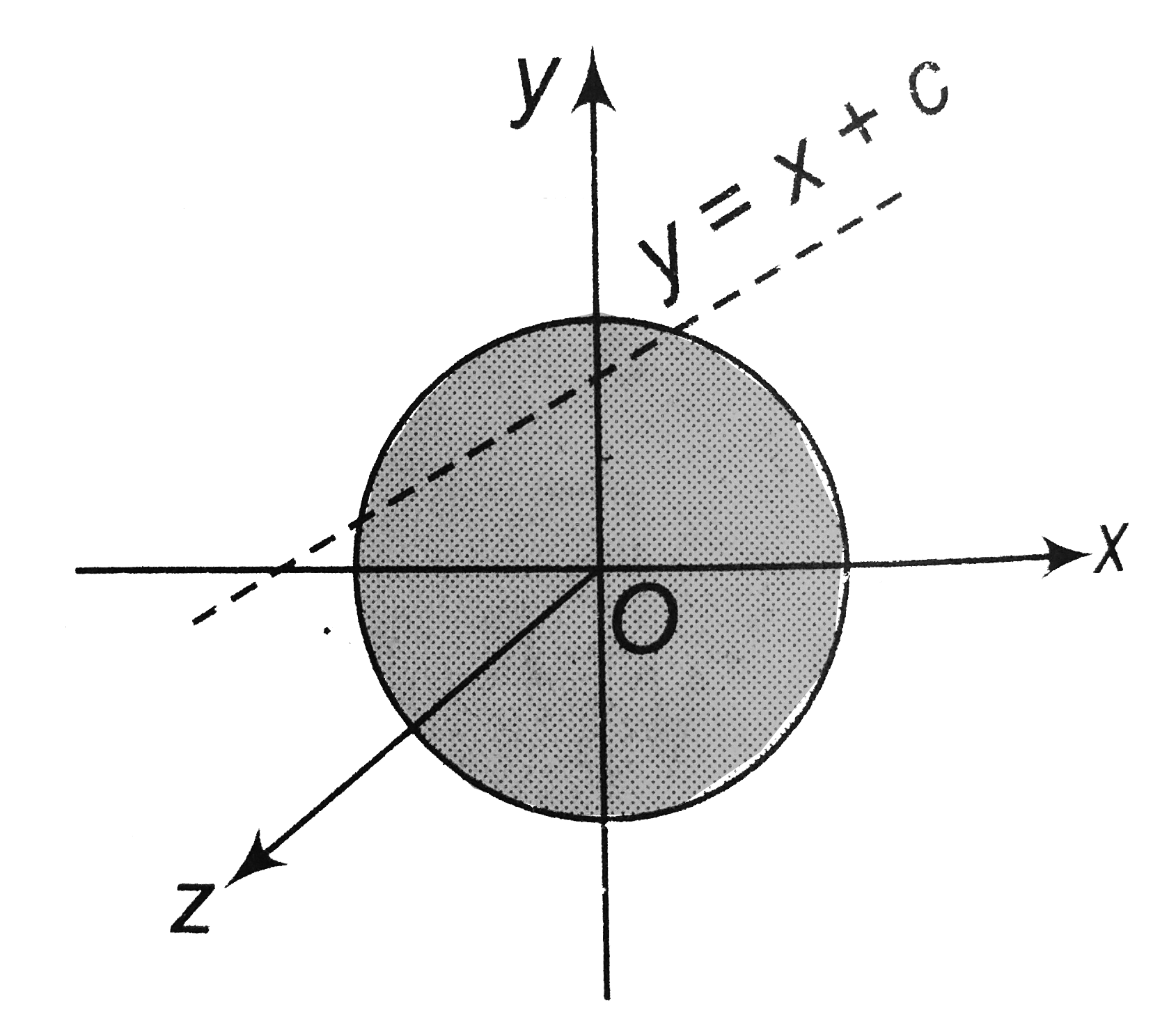 .
.
View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

View Solution
Knowledge Check
The adjoining figure shows a disc of mass M and radius R lying in the X-Y plane with its centre on X - axis at a distance a from the origin. Then the moment of inertia of the disc about the X-axis is
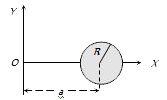 AM(R22)BM(R24)CM(R24+a2)DM(R22+a2)
AM(R22)BM(R24)CM(R24+a2)DM(R22+a2)A uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
 .A−R2B±R√2C+R4D−R
.A−R2B±R√2C+R4D−RA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is
 A−52mR2ωˆkB73mR2ωˆkC−92mR2ωˆkD52mR2ωˆk
A−52mR2ωˆkB73mR2ωˆkC−92mR2ωˆkD52mR2ωˆk
A uniform disc of radius R lies in x-y plane with its centre at origin. Its moment of inertia about the axis x=2R and y=0 is equal to the moment of inertia about the axis y=d and z=0, where d is equal to
View SolutionA circular hole of radius R/2 is cut from a circular disc of radius R. The disc lies in the xy-plane and its centre coincides with the origin. If the remaining mass of the disc is M, then
a. determine the initial mass of the disc and
b. determine its moment of inertia about the z-axis.
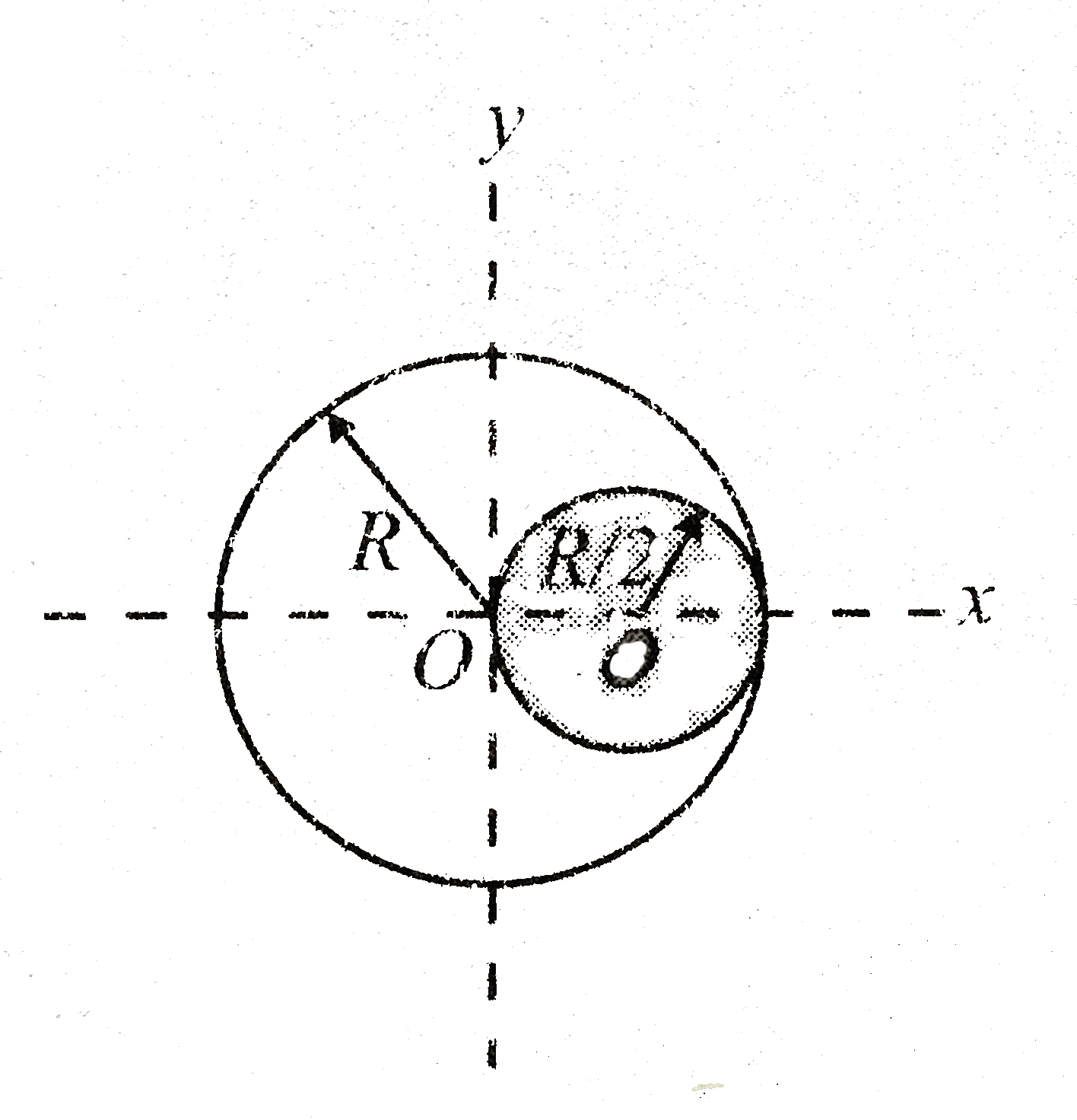
View SolutionA circular hole of radius R/2 is cut from a circular disc of radius R. The disc lies in the xy-plane and its centre coincides with the origin. If the remaining mass of the disc is M, then
a. determine the initial mass of the disc and
b. determine its moment of inertia about the z-axis.
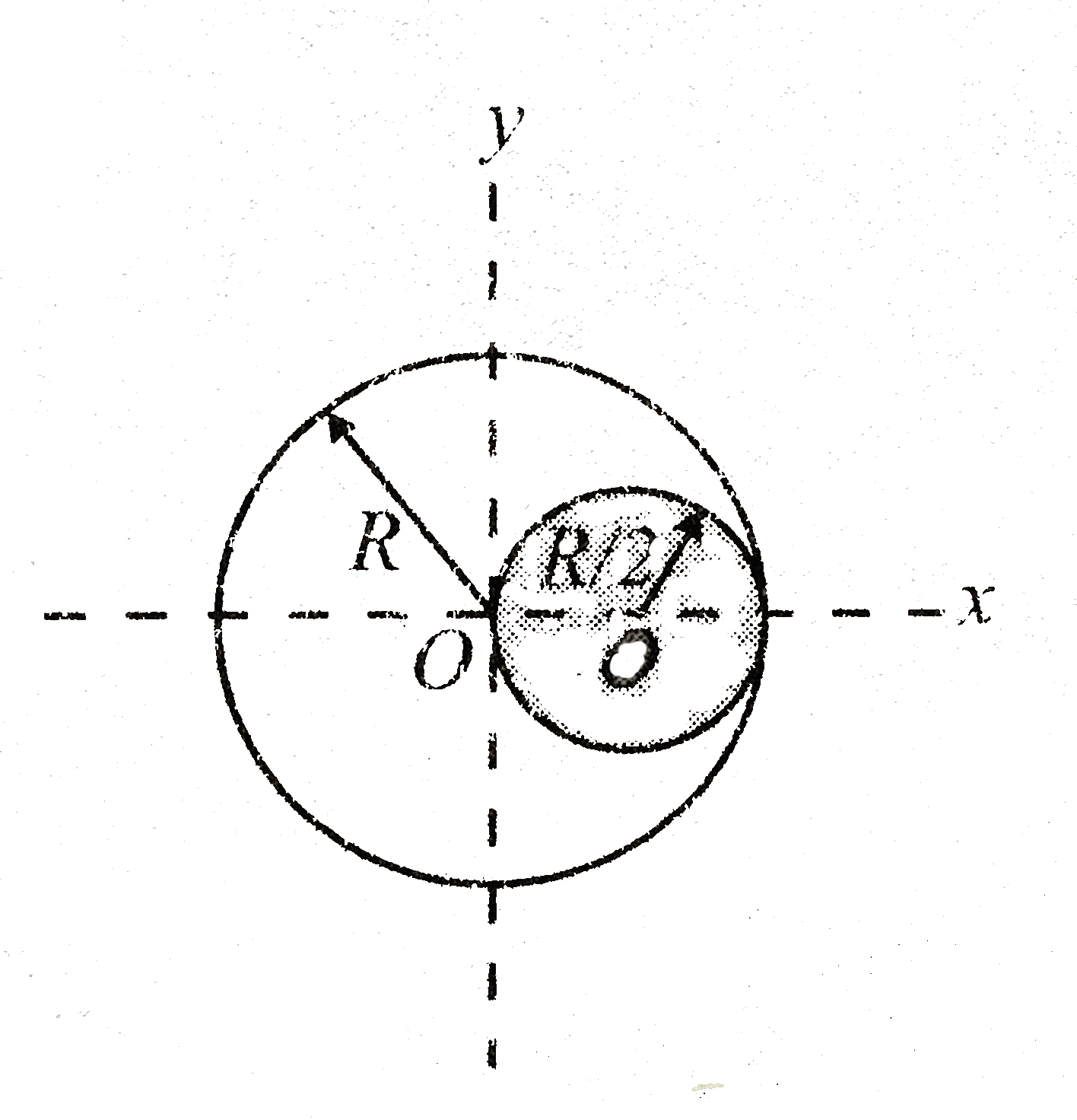
View SolutionRadius of a circle is 5. It cuts x-axis at two points at a distance 3 from the origin. Its centre is
View SolutionA uniform disc of radius R lies in x-y plane with its centre at origin. Its moment of inertia about the axis x=2R and y=0 is equal to the moment of inertia about the axis y=d and z=0, where d is equal to
View Solution
