Out of a disc of mass M and radius R a concentric disc of mass m and radius r is removed. The M.I. of the remaining part about the symmetric axis will be :
(M−m)(R+r)2/2
(M−m)(R2−r2)/2
(M−m)(R−r)2/2
(M−m)(R2+r2)/2
The correct Answer is:D
To find the moment of inertia of the remaining part of the disc after removing a concentric disc, we can follow these steps:
Step 1: Understand the Problem
We have a larger disc of mass M and radius R. From this disc, a smaller concentric disc of mass m and radius r is removed. We need to find the moment of inertia of the remaining part about the symmetric axis.
Step 2: Moment of Inertia of the Full Disc
The moment of inertia I1 of a full disc about its symmetric axis is given by the formula:
I1=12MR2
Step 3: Moment of Inertia of the Removed Disc
The moment of inertia I2 of the smaller disc that is removed is given by:
I2=12mr2
Step 4: Moment of Inertia of the Remaining Part
The moment of inertia I of the remaining part after removing the smaller disc is calculated as:
I=I1−I2
Substituting the expressions for I1 and I2:
I=12MR2−12mr2
Step 5: Factor Out Common Terms
We can factor out 12:
I=12(MR2−mr2)
Step 6: Conclusion
Thus, the moment of inertia of the remaining part about the symmetric axis is:
I=12(MR2−mr2)
We have a larger disc of mass M and radius R. From this disc, a smaller concentric disc of mass m and radius r is removed. We need to find the moment of inertia of the remaining part about the symmetric axis.
The moment of inertia I1 of a full disc about its symmetric axis is given by the formula:
I1=12MR2
The moment of inertia I2 of the smaller disc that is removed is given by:
I2=12mr2
The moment of inertia I of the remaining part after removing the smaller disc is calculated as:
I=I1−I2
Substituting the expressions for I1 and I2:
I=12MR2−12mr2
We can factor out 12:
I=12(MR2−mr2)
Thus, the moment of inertia of the remaining part about the symmetric axis is:
I=12(MR2−mr2)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ENABLE
50 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EFFICIENT
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
Figure shows a hemispherical shell of mass M and radius R and a concentric shell of mass m and radius 3R/4.

View SolutionFrom a circular disc of mass M and radius R, a part of 60∘ is removed. The M.I. of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is

View Solution
Knowledge Check
From a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
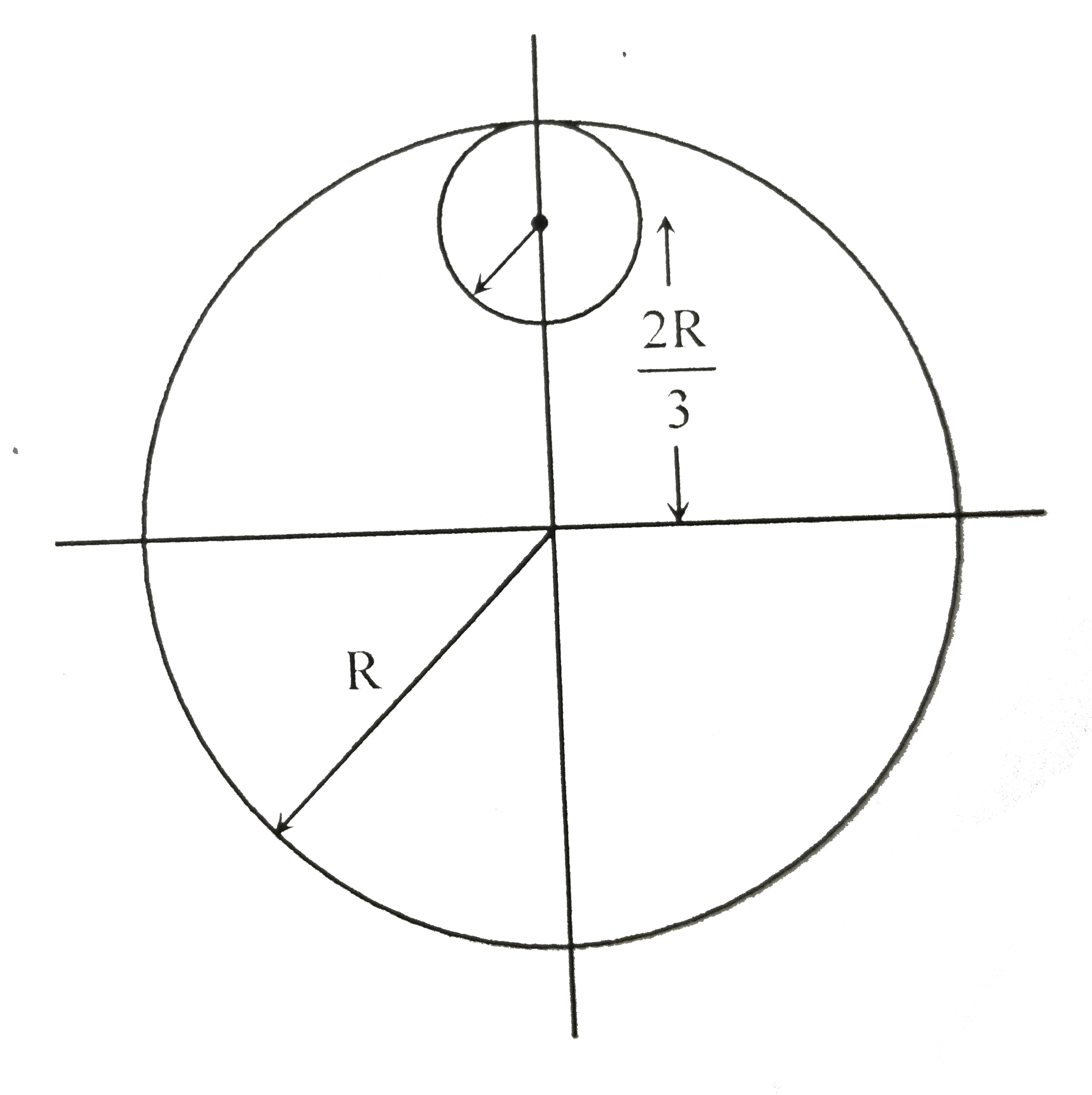 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
Four similar point masses (each of mass m) are placed on the circumference of a disc of mass M and radius R. The M.I. of the system about the normal axis through the centre O will be:
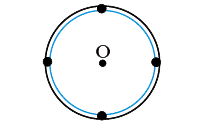
View SolutionA concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
View SolutionA concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
View SolutionA disc of radius r is removed from the centre of a disc of mass M and radius R. The M.I. About the axis through the centre and normal to the plane will be:
View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View SolutionA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View Solution
