A sphere is perfroming pure rolling a shown in the figure. The radius of curvature of trajectory of point A in the shown position is XR. Find 2x.
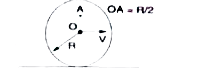
3
4
1
0
The correct Answer is:A
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - VI) Rolling (More than One correct answer Type Questions)3videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - VI) Rolling (Linked Comprehension Type Questions)5videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - V) Angular Impulse Rod-Particle Collisions (Integer Type Quetions)3videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)6videos
RIVISION EXERCISE
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers20videos
ROTATIONAL MECHANICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A uniform disc is having a pure rolling motion on a moving plank as shown in the figure. Choose the correct option among the following .
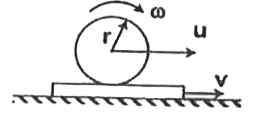 Au−rω=−vBu−rω−v=0C−u=rω+vDnone of above
Au−rω=−vBu−rω−v=0C−u=rω+vDnone of above
A solid sphere of mass M and radius R is in pure rolling as shown in figure. The angular momentum of the sphere about the origin is (linear velocity of centre of mass is v0, in positive x-direction)
View SolutionThe uniform solid sphere shown in the figure has a spherical hole in it. Find the position of its centre of mass.
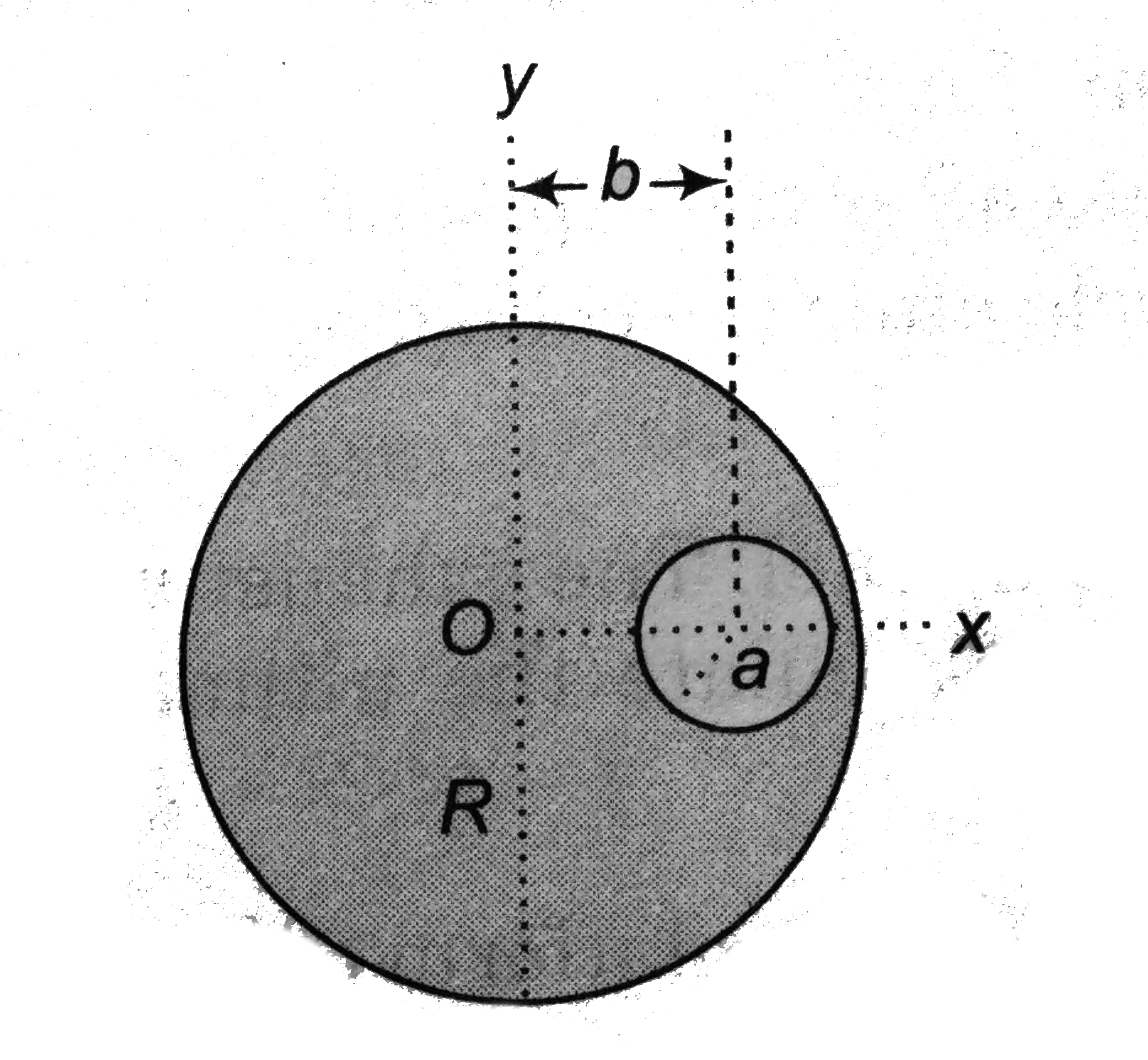 View Solution
View SolutionThe uniform solid sphere shown in the figure has a spherical hole in it. Find the position of its centre of mass.
 View Solution
View SolutionA uniform disc is having a pure rolling motion on a moving plank as shown in the figure. Choose the correct option among the following .
 View Solution
View SolutionA disc of mass m and radius R is rolling without slipping as shown in the figure. The magnitude of net velocity of the point P is (OP=R2)
View SolutionThe variation of pressure versus volume is shown in the figure. The gas is diatomic and the molar specific heat capacity for the process is found to xR. Find the value of x.
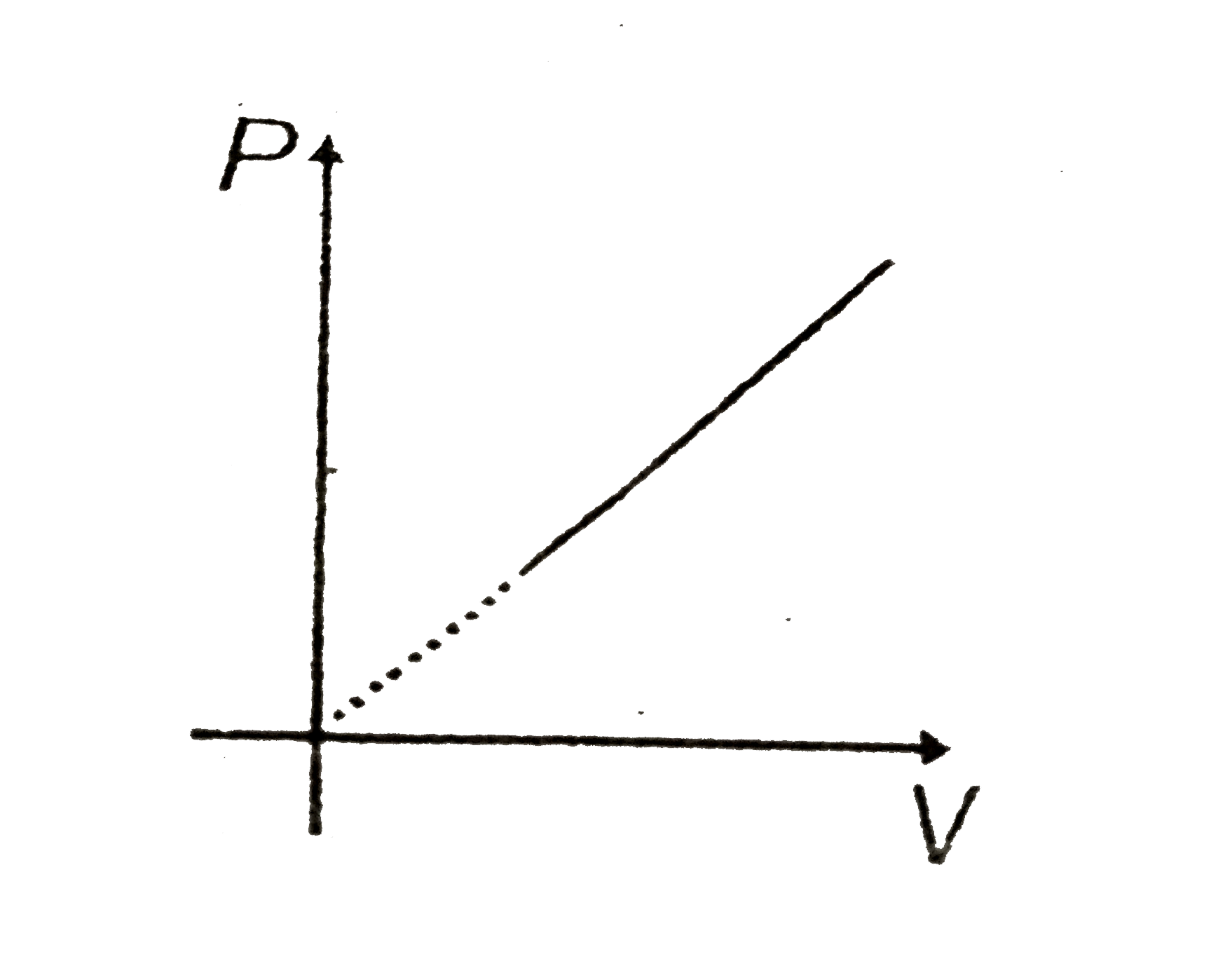 .View Solution
.View SolutionThe variation of pressure versus volume is shown in the figure. The gas is diatomic and the molar specific heat capacity for the process is found to xR. Find the value of x.
 .View Solution
.View Solution


