A solid sphere linear velocity V0=4m/s and angular velocity ω0=9 rad/s as shown. Ground on which it is moving is smooth. It collides (e=1) with rough wall of coefficient of friction μ. Radius of sphere is 1m and mass is 2kg.

If the sphere rolls without slipping after collision, μ=0.25
Angular velocity after collision is 4 rad/s clock wise
Angular velocity after collision is 4 rad/s clock wise
If the sphere rolls without slipping after collision, μ=0.5
The correct Answer is:A, B
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - IV) (LEVEL - II Linked Comprehension Type Questions)
5 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - IV) (LEVEL - II Matrix Matching Type Questions)
2 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - IV) (LEVEL - II Straight Objective Type Questions)
4 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
A solid sphere has linear velocity v0=4 m/s and angular velocity ω0=9 rad/s as shown. Ground on which it is moving , is smooth . It collides elastically with a rough wall of coefficient of friction μ . Radius of the sphere is 1m and mass is 2 kg .

If the sphere after colliding with the wall rolls without slipping on opposite direction, then coefdicient of friction μ is
View SolutionA solid sphere has linear velocity v0=4 m/s and angular velocity ω0=9 rad/s as shown. Ground on which it is moving , is smooth . It collides elastically with a rough wall of coefficient of friction μ . Radius of the sphere is 1m and mass is 2 kg .

What is net linear impulse imparted by the wall on the sphere during impact ?
View Solution
Knowledge Check
A solid sphere has linear velocity v0=4 m/s and angular velocity ω0=9 rad/s as shown. Ground on which it is moving , is smooth . It collides elastically with a rough wall of coefficient of friction μ . Radius of the sphere is 1m and mass is 2 kg .

If the sphere after colliding with the wall rolls without slipping on opposite direction, then coefdicient of friction μ isA12B23C13D14A solid sphere has linear velocity v0=4 m/s and angular velocity ω0=9 rad/s as shown. Ground on which it is moving , is smooth . It collides elastically with a rough wall of coefficient of friction μ . Radius of the sphere is 1m and mass is 2 kg .

What is net linear impulse imparted by the wall on the sphere during impact ?A√32N−sB4√17N−sC4√5N−sD15√2N−sA solid sphere with a velocity (of centre of mass) v and angular velocity ω is gently placed on a rough horizontal surface. The frictional force on the sphere :
Amust be forward (in direction of v)Bmust be backward (opposite to v)Ccannot be zeroDnone of the above
A solid sphere has linear velocity v0=4m/s and angular velocity ω0=9 rad/s as shown . Ground on which it is moving , is smooth . It collides elastically with a rough wall of coefficient with a rough wall of coefficient of friction μ. Radius of the sphere is 1 m and mass is 2 kg.
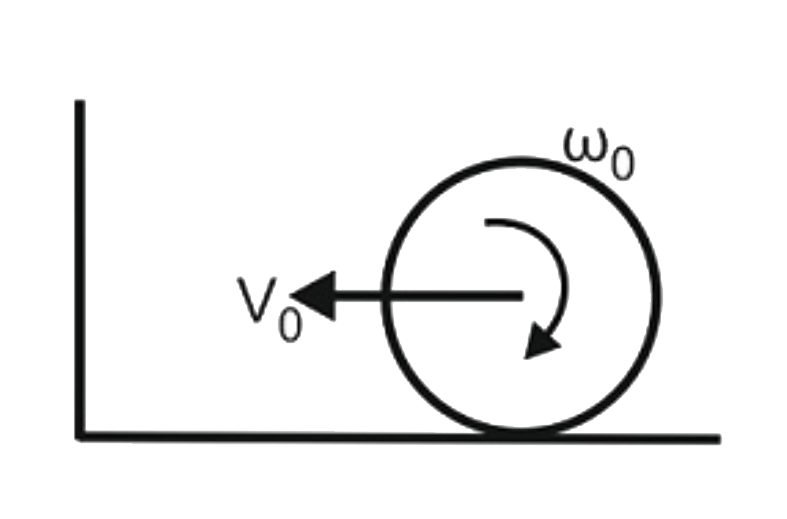
If the sphere after colliding with the wall rolls without slipping in opposite direction, the coefficient of friction μ is
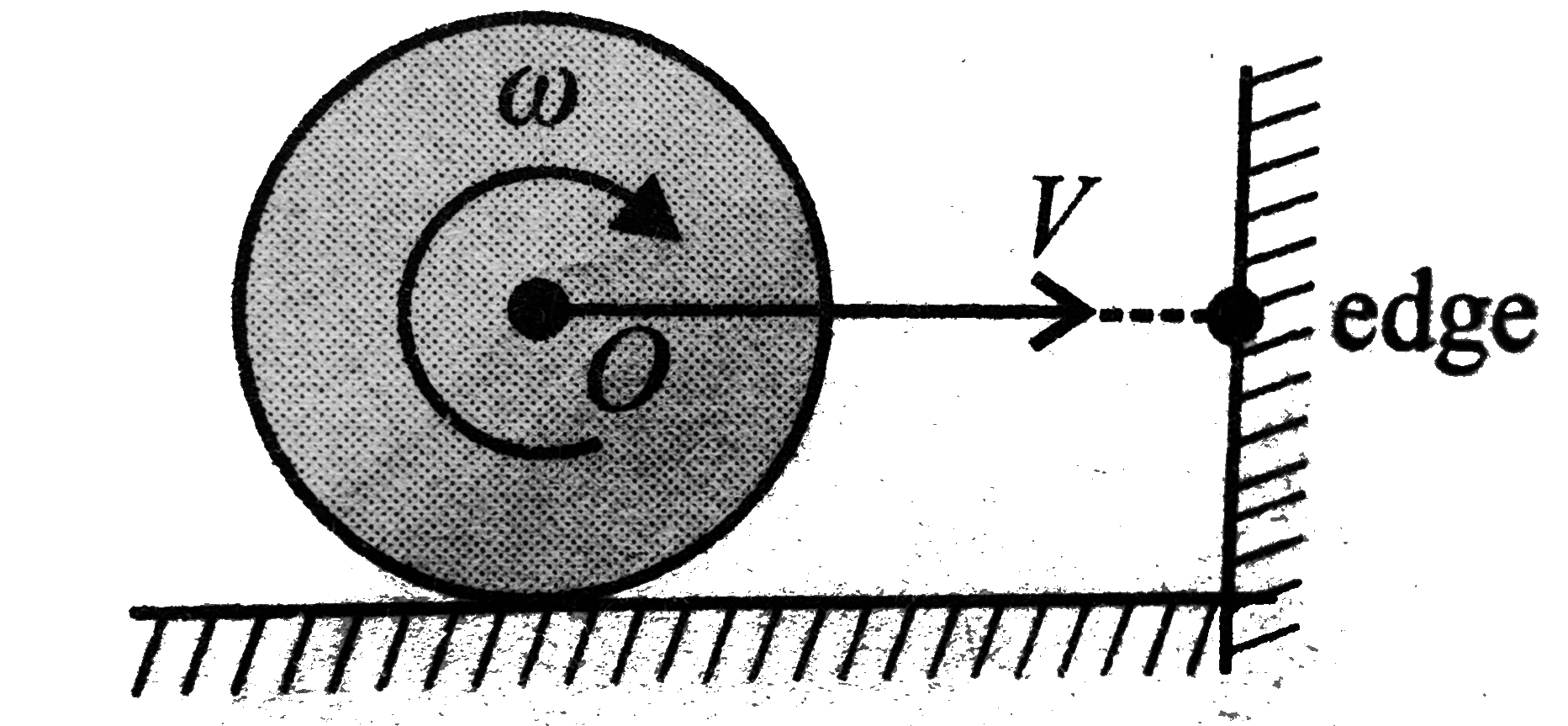
View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
View SolutionA sphere is moving on a smooth surface with linear speed v0 and angular velocity ω0. It finds a rough inclined surface and it starts climbing up:

View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity v and angular velocity ω=(v=ωr). The sphere collides with a sharp edge on the wall as shown in figure. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the surface just after the collision is equal to

View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω=(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to

View Solution
