A uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
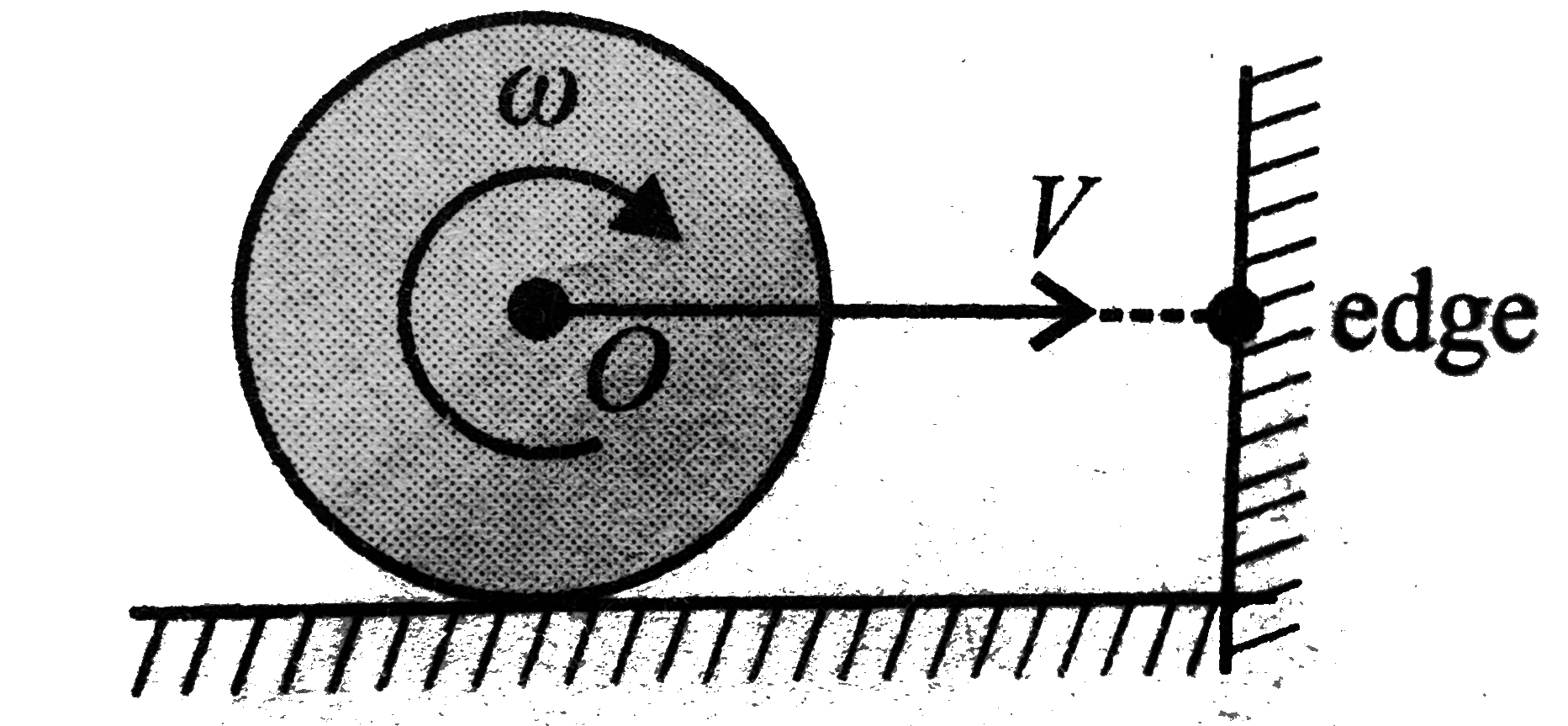
V
V5
3V5
V6
The correct Answer is:A
Impulse provided by the edge in the horizontal direction
∫Ndt=−mV'−(mV)..i
Friction impulse in the vertical direction
μR∫Ndt=25mr2(VR)…….ii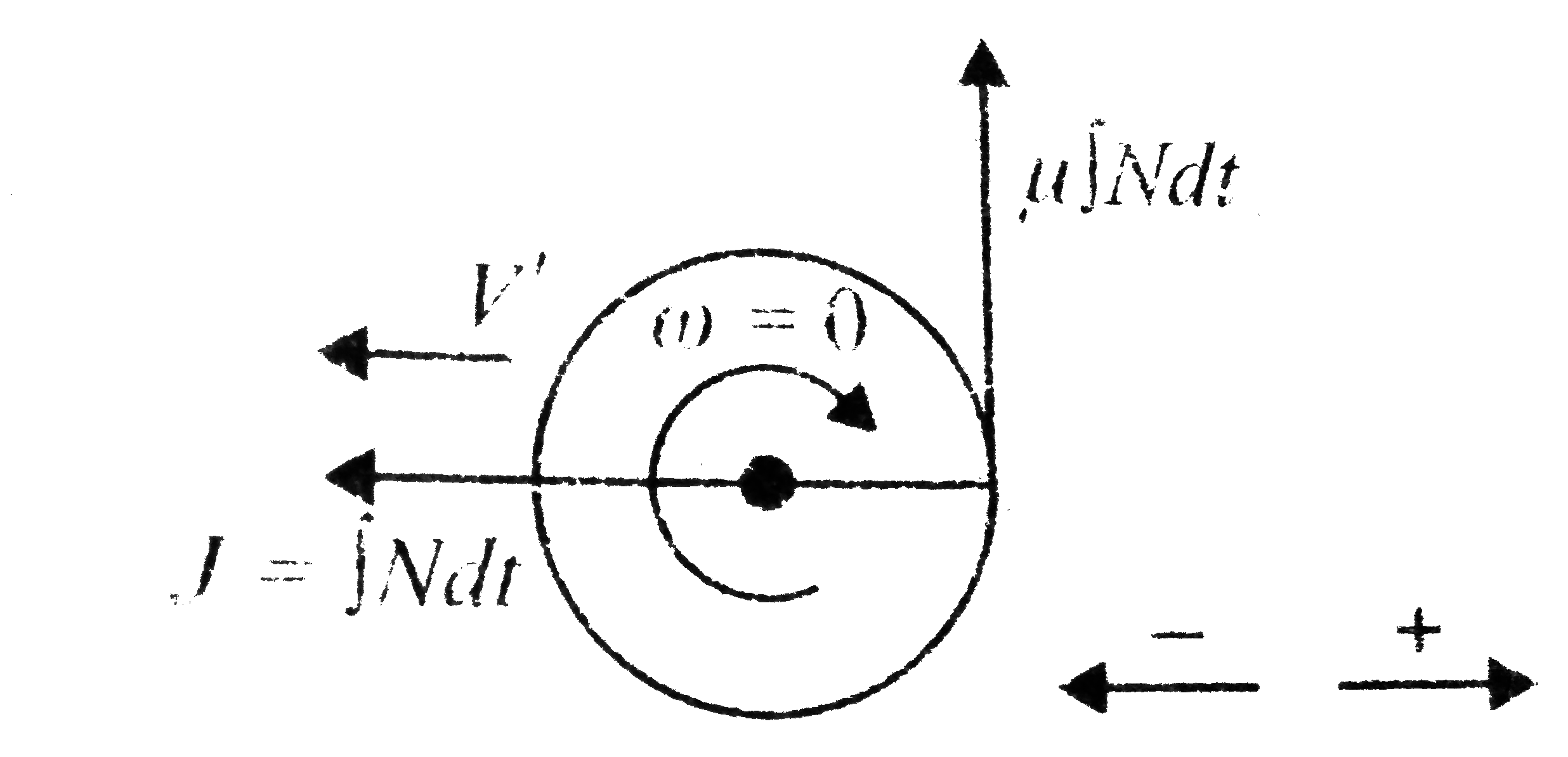 
Form eqn i annd ii we get
∫Ndt=2mV and V'=V
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A sphere is projected up an inclined plane with a velocity v0 and zero angular velocity as shown. The coefficient of friction between the sphere and the plane is μ=tanθ.. Find the total time of rise of the sphere.
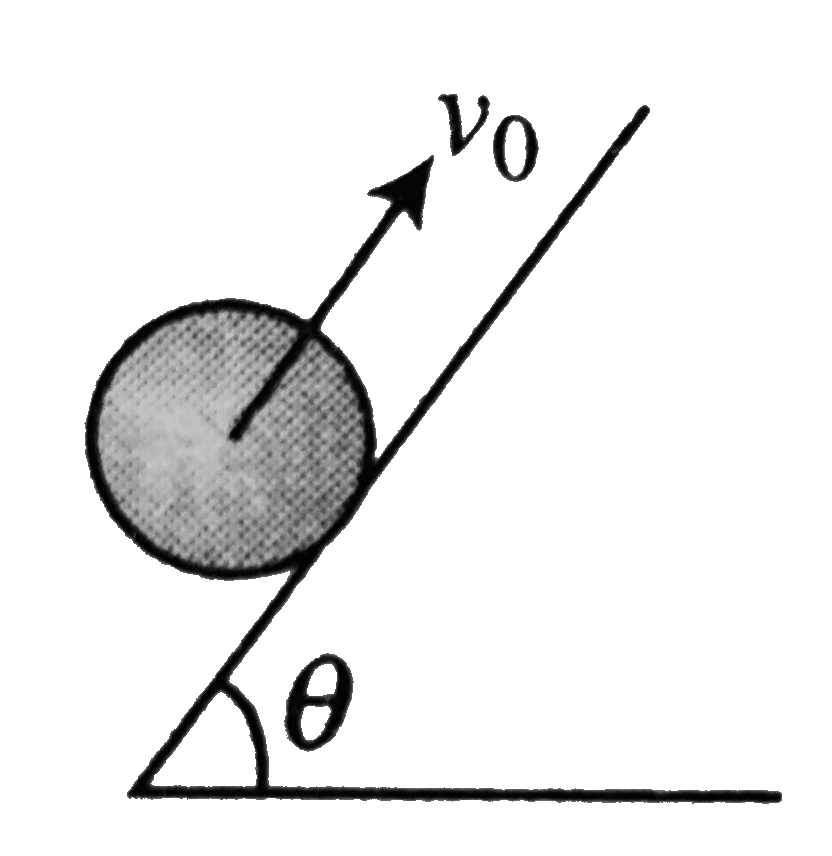View SolutionA uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity v0 and an angular velocity ω0 as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
View SolutionA sphere of mass m moving with velocity v collides head-on with another sphere of the same mass at rest. If the coefficient of resistitution e=1/2, then what is the ratio of final velocity of the second sphere to the intial velocity of the first sphere ?
View SolutionA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that
View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.
View SolutionA smooth sphere is moving on a horizontal surface with velocity vector 2ˆi+2ˆj immediately before it hits a vertical wall. The wall is parallel to ˆj and the coefficient of restitution of the sphere and the wall is e=12. Find the velocity of the sphere after it hits the wall?
View SolutionA uniform solid sphere A of mass m is rolling without sliding on a a smooth horizontal surface. It collides elastically and head - on with another stationary hollow sphere B of the same mass and radius. Assuming friction to be absent everywhere, the ratio of the kinetic energy of B to that of A just after the collision is
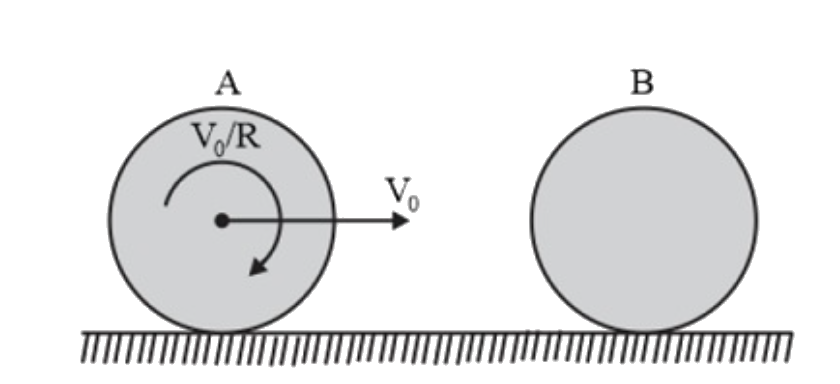View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
Find the displacement of the plank till the sphere starts pure rolling.View Solution