A thin disc of radius R and mass M is free to rotate about a vertical axis passing through its centre and perpendicular to its plane. The disc in initially at rest. A small of mass M/3 is walking along the rim of the disc with a relative speed 'v' with respect to the surface of the disc. What is the angular velocity with which the disc rotates in the opposite direction ?
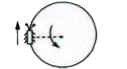
v5R
2v5R
v3R
2v3R
The correct Answer is:B
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) More than One correct answer Type Questions
15 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Linked comprehension Type Questions
14 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Integer Type Questions
32 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
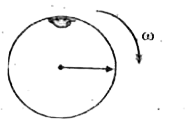
View SolutionA disc of radius R and mass m is mounted on a vertical axis through its centre and perendicular to its plane. A rat of same mass m runs around the rim of the disc with speed v anticlockwise relative to stationary observer. The disc rotates clockwise with angular speed omega. The rat finds a piece of bread on the rim and stops. Find the angular velocity of the disc after the rat stops.
View Solution
Knowledge Check
A disc of mass 2 kg and diameter 40 cm is free to rotate about an axis passing through its centre and perpendicular to its plane. If a force of 50 N is applied to the disc tangentially Its angular acceleration will be
A100rad/s2B25rad/s2C250rad/s2D500rad/s2A disc of mass 4 kg and radius 0.2 m, makes 20 rev/s, about an axis passing through its centre and perpendicular to the plane of the disc. The angular momentum of the disc is approximately equal to
A10 kg-m2/secB5 kg-m2/secC15 kg-m2/secD20 kg-m2/secA disc of radius 10 cm can rotate about an axis passing through its centre and perpendicular to its plane. A force of 10 N is applied along the tangent in the plane of the disc. If the moment of inertia of the disc about its centre is 5kgm2, then the increase in the angular velocity of the disc in 10 s will be
A2 rad/sB4 rad/sC1 rad/sD50 rad/s
A disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. Another disc of same dimensions but of mass M/4 is placed gently on the first disc coaxially. The angular velocity of the system now is
View SolutionA thin and circular disc of mass m and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . If another disc of same dimension but mass ml4 is placed gently on the first disc co-axially, then the new angular velocity of the system is
View Solution
