A ring of radius R rolls without sliding with a constant velocity. The radius of curvature of the path followed by any particle of the ring at-the highest point its path will be :
R
2R
4R
8R
The correct Answer is:C
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) More than One correct answer Type Questions
15 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Linked comprehension Type Questions
14 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Integer Type Questions
32 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions

A ring of radius R rolls without slipping on a rough horizontal surface with a constant velocity. The radius of curvature of the path followed by any particle of the ring at the highest point of its path will be :
View SolutionA wheel of radius R is rolling without sliding uniformly on a horizontal surface. Find the radius of curvature of the path of a point on its circumference when it is at highest point in its path.
View Solution
Knowledge Check
A ring of radius R rolls without slipping on a rough horizontal surface with a constant velocity. The radius of curvature of the path followed by any particle of the ring at the highest point of its path will be :
 .ARB2 RC4 RDnone of these
.ARB2 RC4 RDnone of theseThe radius of curvature of the path of a charged particle moving in a static uniform magnetic field is
ADirectly propotional to the magnitude of the charge on the particleBDirectly propotional to the magnitude of the liner momentum of the particleCDirectly proportional to the kinetic energy of the particleDInversely proportional to the magnitude of the magnetic fieldThe radius of curvature of the path of a charged particle moving in a static uniform magnetic field is
ADirectly proportional to the magnitude of the charge on the particleBDirectly proportional to the magnitude of the linear momentum of the particleCDirectly proportional to the kinetic energy of the particleDInversely proportional to the magnitude of the magnetic field
A conducting ring of radius 'r' is rolling without slipping with a constant angular velocity ω (figure). If the magnetic field strengh is B and is directed into the page the emf induced across PQ is
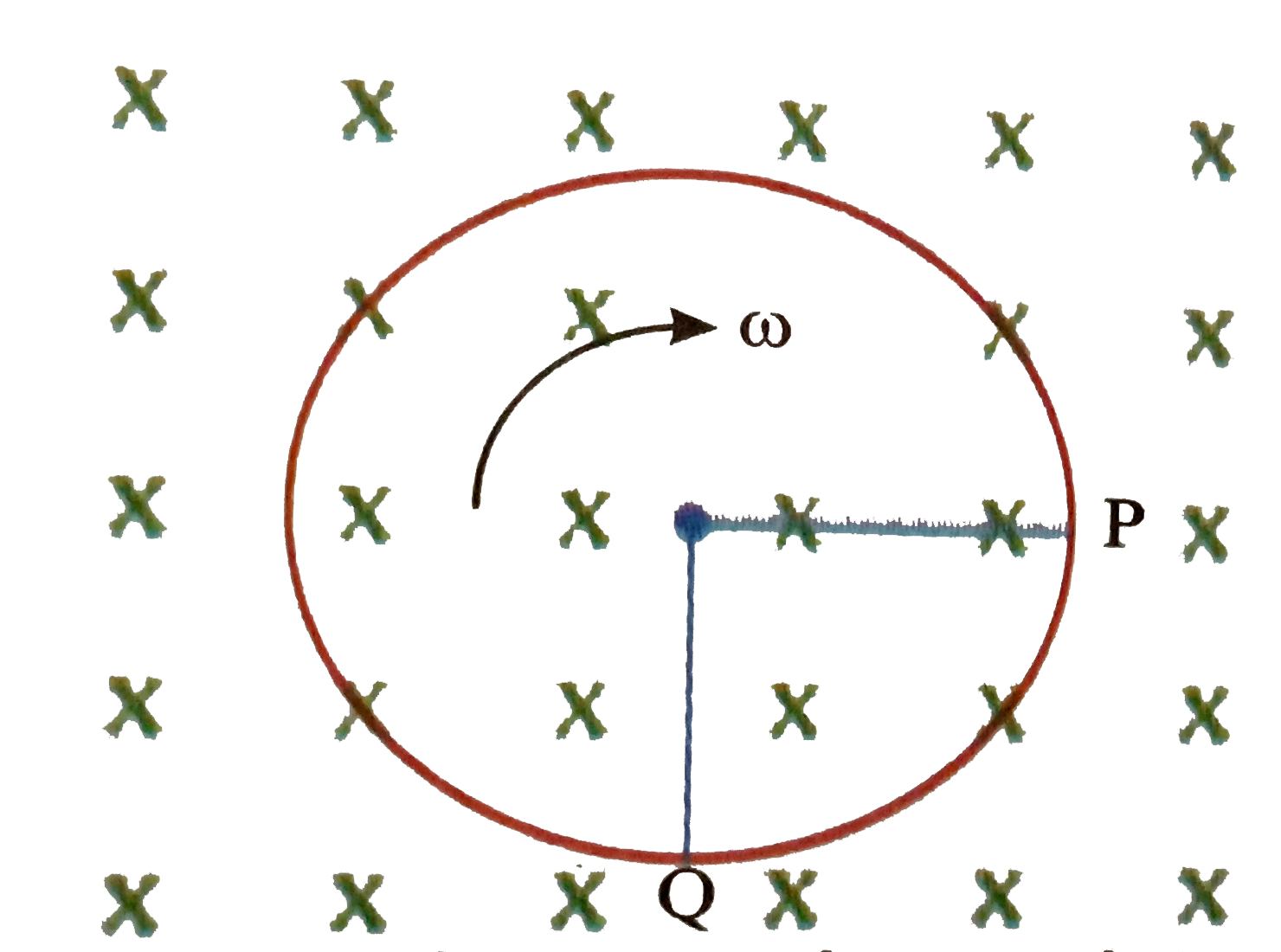
View SolutionThe radius of curvature of the path of a charged particle in a uniform magnetic field is directly proportional to
View SolutionThe radius of curvature of the path of the charged particle in a uniform magnetic field is directly proportional to
View SolutionA conducting ring of radius 'r' is rolling without slipping with a constant angular velocity ω (figure). If the magnetic field strengh is B and is directed into the page the emf induced across PQ is

View SolutionA wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
View Solution
