A smooth sphere of radius R is fixed on a horizontal surface. A steel, moving horizontally with velocity v0=5√gR, collides with the sphere, changes its direction and moves with velocity v as shown. Then
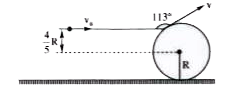
4√2v0=5√3v
8v0=5√3v
5v0=8√3v
v=v0
The correct Answer is:B
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) More than One correct answer Type Questions
15 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Linked comprehension Type Questions
14 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Integer Type Questions
32 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
A small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration a0=g. The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is

View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
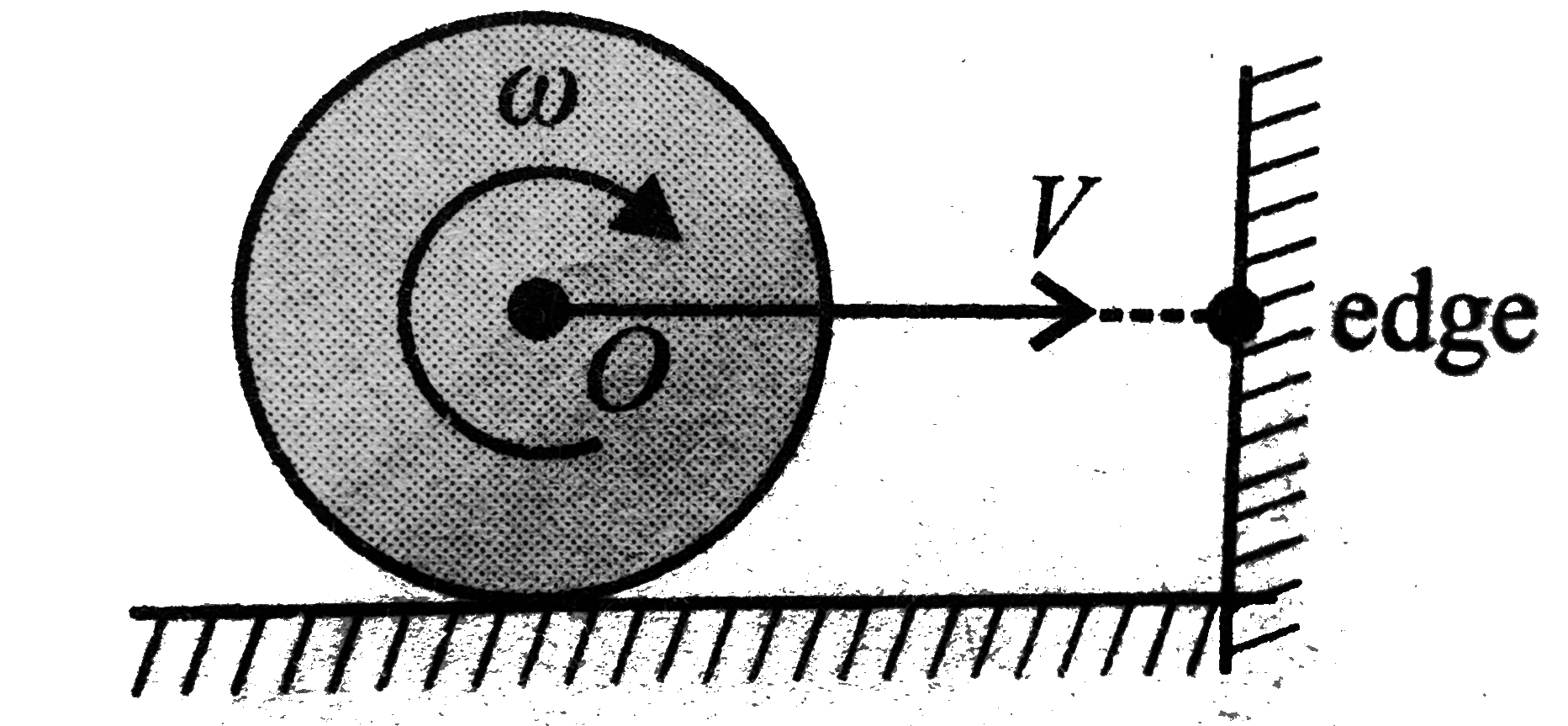
View Solution
Knowledge Check
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.A small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration a0=g. The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is
 A√gR3B√2gR3C√5gR3D√7gR3
A√gR3B√2gR3C√5gR3D√7gR3A uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity v and angular velocity ω=(v=ωr). The sphere collides with a sharp edge on the wall as shown in figure. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the surface just after the collision is equal to
 AvBv5C3v5Dv6
AvBv5C3v5Dv6
A solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
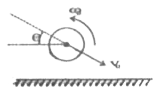
View SolutionA uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity v0 and an angular velocity ω0 as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
View Solution(i) A solid sphere of radius R is released on a rough horizontal surface with its top point having thrice the velocity of its bottom point A (VA=V0) as shown in figure. Calculate the linear velocity of the centre of the sphere when it starts pure rolling.
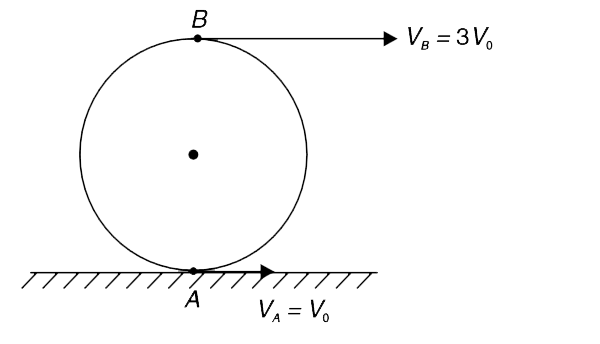
(ii) Solid sphere of radius R is placed on a rough horizontal surface with its centre having velocity V0 towards right and its angular velocity being ω0 (in anticlockwise sense). Find the required relationship between V0 and ω0 so that -
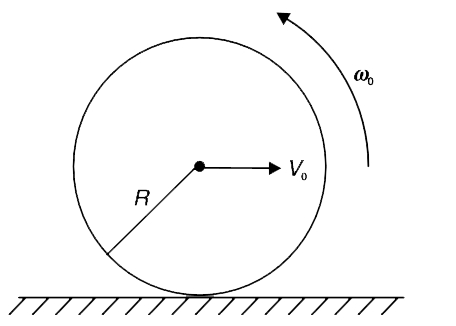
(a) the slipping ceases before the sphere loses all its linear momentum.
(b) the sphere comes to a permanent rest after some time.
(c) the velocity of centre becomes zero before the spinning ceases.
View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω=(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to

View SolutionA solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may

View Solution
