A uniform disc of mass m and radius R starts with velocity V0 on rough horizontal floor with a purely sliding motion at t=0 as shown. At t=t0, disc starts rolling without sliding. Then (Coefficient of frictions is μ)

Net work done by frictional force upto time t<t0 is given by mμgt2(3μgt−2V0)
Net work done by friction force upto time t<t0 is given by mμgt2(2μgt−V0)
Net work done by frictional force upto time t=2t0 is given by mμgt0(2μgt0−V0)
Net work done by friction force upto time t=2t0 is given by mμgt02(3μgt0−2V0)
The correct Answer is:A, D
Topper's Solved these Questions
- ROTATIONAL DYNAMICS Book:AAKASH SERIESChapter:ROTATIONAL DYNAMICS Exercise:PRACTICE SHEET (ADVANCED) Linked comprehension Type Questions
Explore 14 Videos
- ROTATIONAL DYNAMICS Book:AAKASH SERIESChapter:ROTATIONAL DYNAMICS Exercise:PRACTICE SHEET (ADVANCED) Matrix Matching Type Questions
Explore 2 Videos
- ROTATIONAL DYNAMICS Book:AAKASH SERIESChapter:ROTATIONAL DYNAMICS Exercise:PRACTICE SHEET (ADVANCED) Straight Objective Type Questions
Explore 37 Videos
- RIVISION EXERCISEBook:AAKASH SERIESChapter:RIVISION EXERCISEExercise:MOTION IN A PLANE (LAMNI.S THEOREM)
Explore 6 Videos
- ROTATIONAL MECHANICSBook:AAKASH SERIESChapter:ROTATIONAL MECHANICSExercise:Questions for Descriptive Answers
Explore 20 Videos
Similar Questions
A uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts with a purely sliding motion at t= 0. After t0 seconds it acquires a purely rolling motion.
(a) Calculate the velocity of the centre of mass of the disc at t0
(b) Assuming the coefficient of friction to be μ, calculate to. Also calculate the work done by the frictional force as a function of time and the total work done by it over a time t muchlonger than t0.
View SolutionA uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts off with a purely sliding motion at t=0. After t0 seconds, it acquires pure rolling motion as shown in the figure.
(a) Calculate the velocity of the center of mass of the disc at t0.
Assuming that the coefficent of friction to be μ, calculate t0.

View Solution
Knowledge Check
A uniform ring of mass 'm' and radius 'R' is projected horizontally with velcoty v0 on a rough horizontal floor, so that it starts off with a purely sliding motion and it acquires a pure rolling motion after moving a distance d. If the coefficient of friction between the ground and ring is μ, then work done by the friction in the process is
A−μmgdB−14mv20CμmgdD−18mv20A uniform disc of mass m and radius R is thrown on horizontal law in such a way that it initially slides with speed V0 without rolling. The distance travelled by the disc till it starts pure rolling is (Coefficient friction between the contact is 0.5)
Av209gB5v209gCv203gD3v208g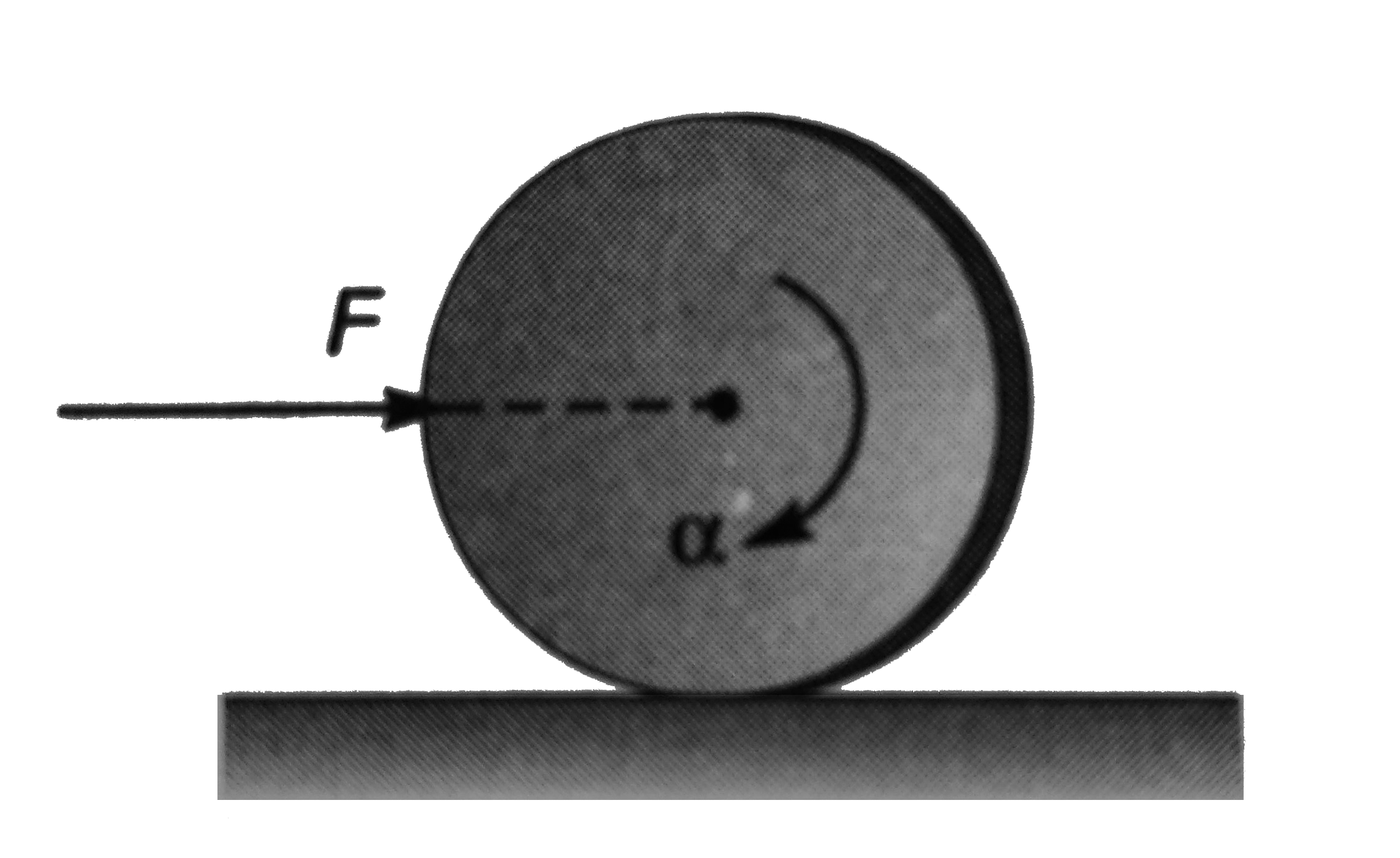
Consider a uniform disc of mass m, radius r rolling without slipping on a rough surface with linear acceleration a and angular acceleration α due to an external force F as shown in the figure coefficient of friction is μ.
Q. The work done by the frictional force at the instant of pure rolling isAμmgat22Bμmgat2)Cμmg(at2)αDzero
A uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts off with a purely sliding motion at t=0. After t0 seconds, it acquires pure rolling motion as shown in the figure.
(a) Calculate the velocity of the center of mass of the disc at t0.
Assuming that the coefficent of friction to be μ, calculate t0.

View SolutionA uniform disk of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts off with a purely sliding motion at t=0. After t0 seconds it acquires a purely rolling motion as shown in figure.
(i) Calculate the velocity of the centre of mass of the disk at t0.

(ii) Assuming the coefficient of friction to be μ calculate t0. Also calculate the work done by the frictional force as a function of time and the total work done by it over a time t much longer than t0.
View SolutionA uniform ring of mass 'm' and radius 'R' is projected horizontally with velcoty v0 on a rough horizontal floor, so that it starts off with a purely sliding motion and it acquires a pure rolling motion after moving a distance d. If the coefficient of friction between the ground and ring is μ, then work done by the friction in the process is
View SolutionA uniform disc of mass m and radius R is thrown on horizontal lawn in such a way that it initially slides with speed V0 without rolling. The distance travelled by the disc till it starts pure rolling is (Coefficient friction between the contact is 0.5)
View SolutionConsider a uniform disc of mass m, radius r rolling without slipping on a rough surface with linear acceleration a and angular acceleration α due to an external force F as shown in the figure coefficient of friction is μ.
Q. The work done by the frictional force at the instant of pure rolling is
View Solution
