Two astronauts each having mass 'm' are connected by a light rope of lengt l0. They are orbiting around their centre of mass with angular speed 'ω0' in free space. Now astronaut - 1 starts collecting rope slowly such that final length of the string between them reduces to l0/2 and becaomes constant (treat astronauts as particle)

Final angular speed of system is 2ω0
Final angular speed of system is 4ω0
Net work done by astronaut-1 in processes is 3ml20ω204
Net work done by astronaut - 1 in processes is 3ml20ω208
The correct Answer is:B, C
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Linked comprehension Type Questions14videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Matrix Matching Type Questions2videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Straight Objective Type Questions37videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)6videos
RIVISION EXERCISE
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers20videos
ROTATIONAL MECHANICS
Similar Questions
Two astronauts having mass of 75kg and 50kg are connected by a rope of length L=10m and negligible mass. They are in space, orbiting their centre of mass at an angular speed of ω0=5rad/s. The centre of mass itself is moving uniformly in space at a velocity of 10m/s. By pulling on the rope, the astronauts shorten the distance between them to L2=5m . How much work is done by the astronauts in shortening the distance between them ? Assuming that the astronauts are athletic and each of them can generate a power of 500 watt, is it possible for the two astronauts to reduce the distance between them to 5m, within a minute?View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
Amω2l0kBmω2l0k−mω2Ckl0k−mω2Dmω2l0k+mω2 - Question 2 - Select One
A block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
Al0mω2k−mω2Bl0mω2k+mω2Cl0mω2k−mωDl0mω2k+mω
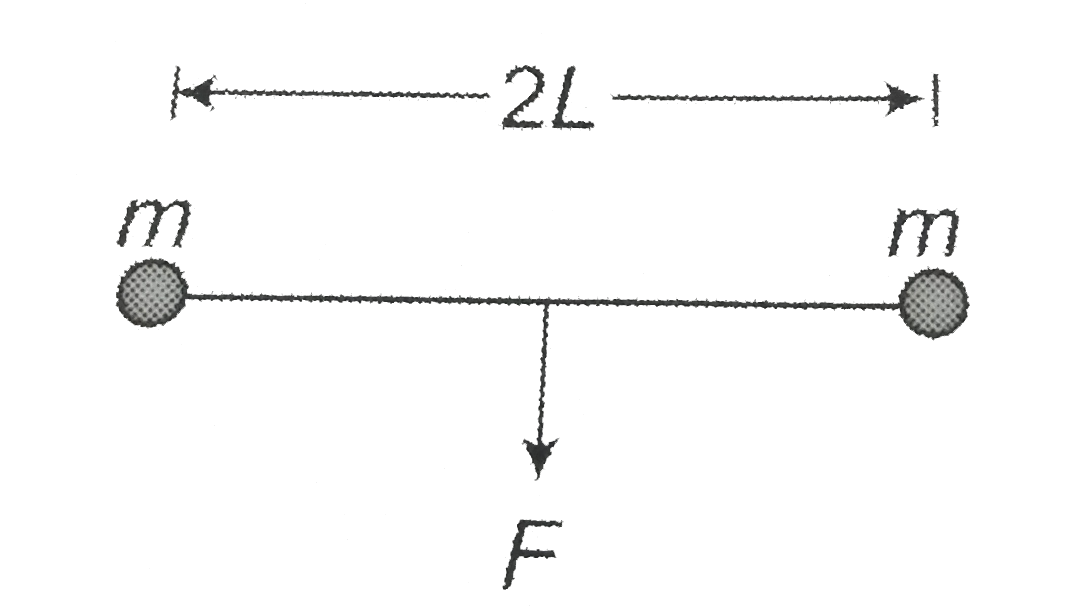
Two particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x
 View Solution
View SolutionA block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
View SolutionTwo particles of masses m1andm2 are joined by a light rigid rod of length r. The system rotates at an angular speed ω about an axis through the centre of mass of the system and perpendicular to the rod. Show that the angular momentum of the system is L=μr2ω where μ is the reduced mass of the system defined as μ=m1m2m1+m2
View SolutionTwo particles of mass m each are attached to a light rod of length d, one at its centre and the other at a free end, The rod is fixed at the other end is rotated in a plane at an angular speed ω. Calculate the angular momentum of the particle at the end with respect to the particle at the centre
View SolutionTwo particles of mass m each are attached to a light rod of length d, one at its centre and the other at a free end, The rod is fixed at the other end and is rotated in a plane at an angular speed ω. Calculate the angular momentum of the particle at the end with respect to the particle at the centre
View SolutionA thin circular right of mass M and radius R is rotating about its axis with an angular speed ω0 two particles each of mass m are now attached at diametrically opposite points. Find new angular speed of the ring.
View Solution

