Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If √8R is the distance between the centres of a ring (of mass 'm') and a sphere (mass "M") where both have equal radius "R'
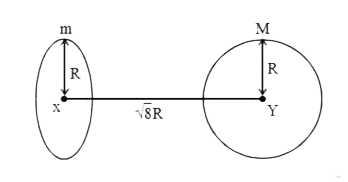
√89.GmMR
2√23.GMmR2
13√8.GMmR2
√827.GmMR2
The correct Answer is:D
Step by step video, text & image solution for Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If sqrt8R is the distance between the centres of a ring (of mass 'm') and a sphere (mass "M") where both have equal radius "R' by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS (SECTION-A)
20 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS SECTION B
30 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
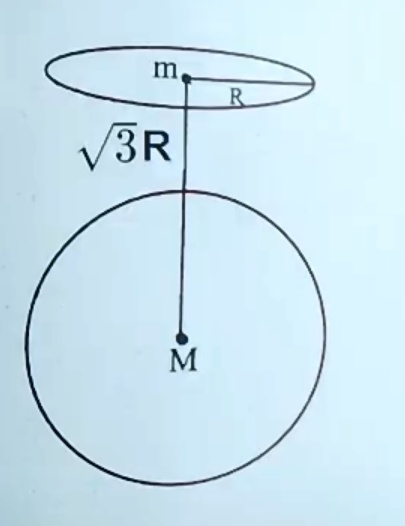
Find the force of attraction between a solid sphere of mass M and a ring of mass m as shown.
View Solutionfind the gravitational force of attraction between a uniform sphere of mass M and a uniform rod of length L and mass m, placed such that r is the distance between the centre of the sphere and the near end of the road.
View Solution
Knowledge Check
The gravitational force of attraction between a uniform sphere of mass M and a uniform rod of length l and mass in as shown in figure is
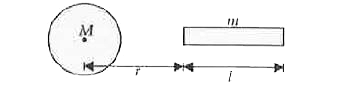 AGMmr(r+1)BGMr2CMm2D(r2+1)mM
AGMmr(r+1)BGMr2CMm2D(r2+1)mMThe escape velocity form the centre of a unifrom ring of mass M and radius R is :
A√2GMRB√GMRC√GM2RD√GMRA ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is
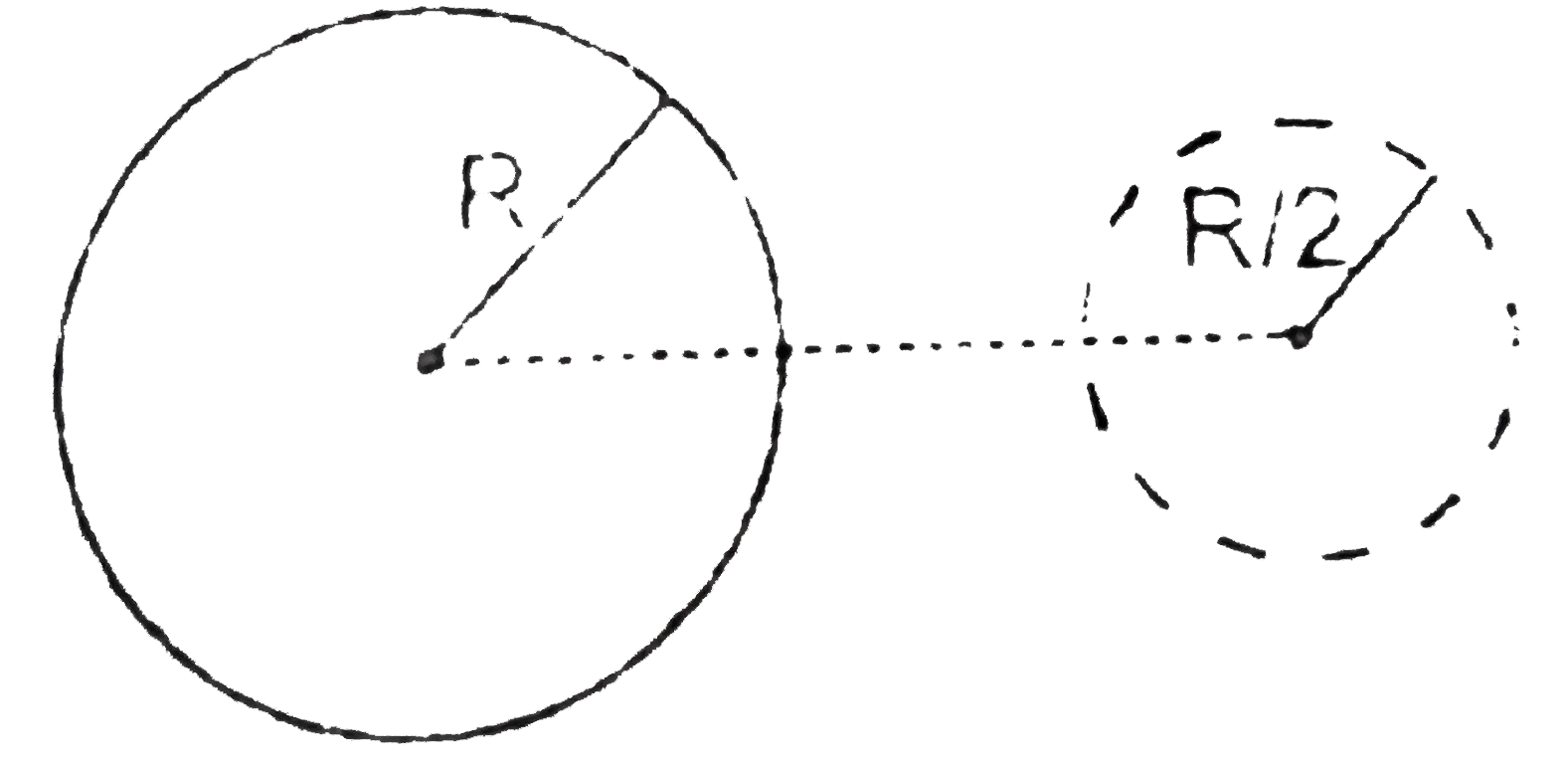 AλR∈0BλR2∈0CλπR4∈0DλπR3∈0
AλR∈0BλR2∈0CλπR4∈0DλπR3∈0
Find potential at a point 'P' at a distance 'x' on the axis away from centre of a uniform ring of mass M and radius R .
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
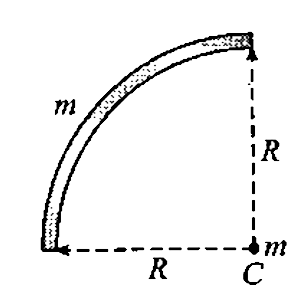
View SolutionFind the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
View SolutionA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
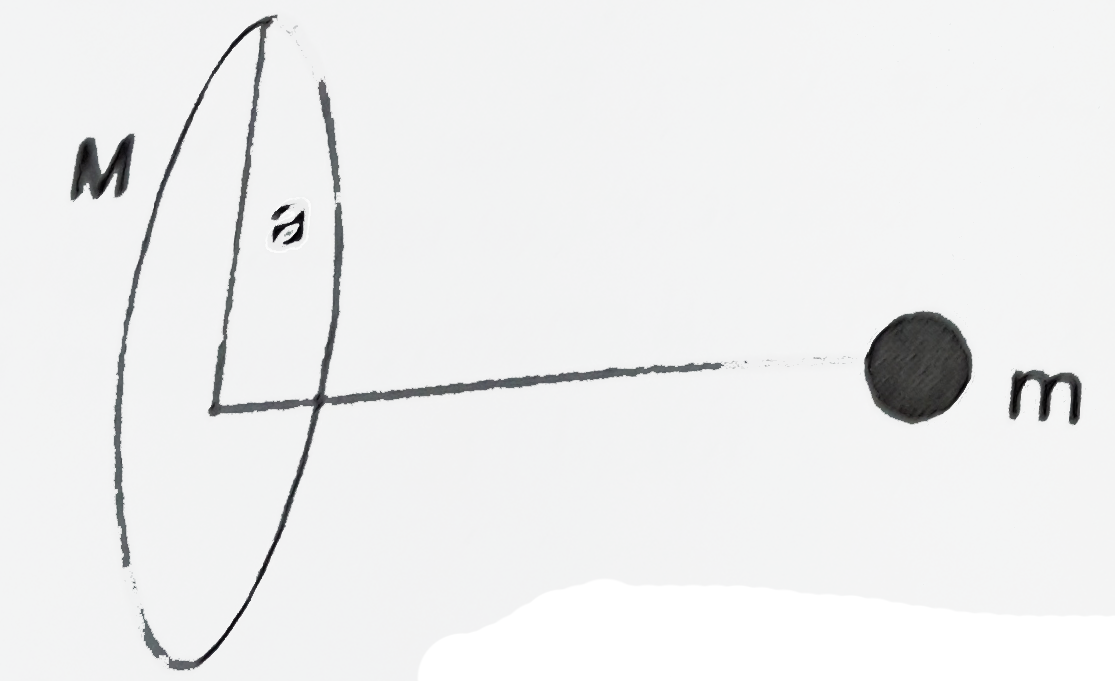
The force, when x=0 :
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View Solution
