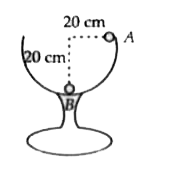
A 2 g ball of glass is released from the edge of a hemispherical cup w

A ball of mass $m$ is released from A inside a smooth wedge of mass $m$ as shown in figure. What is the speed of the wedge when the ball reaches point B?

A(a) ${(\frac{g R}{3 \sqrt{2}})}^{1 / 2}$
B(b) $\sqrt{2 g R}$
C(c) ${(\frac{5 g R}{2 \sqrt{3}})}^{1 / 2}$
D(d) $\sqrt{\frac{3}{2} g R}$
A ball of mass 1 kg is released from position A inside a wedge with a hemispherical cut of radius 0.5 m as shown in figure. The force exerted by the vertical wall OM on wedge, when the ball is in position B is (neglect friction everywhere) (Take $g = 10 m / s^{2}$ )

A10 N
B $5 \sqrt{3} N$
C $\frac{15 \sqrt{3}}{2} N$
D15 N
A ball is dropped from the top of a building the ball takes 0.5 s to fall past the 3 m length of a window at certain distance from the top of the building speed of the ball as it crosses the top edge of the window is $(g = 10 m / s^{2})$
A $3.5 m s^{- 1}$
B $8.5 m s^{- 1}$
C $5 m s^{- 1}$
D $12 m s^{- 1}$

A 2 g ball of glass is released from the edge of a hemispherical cup whose radius is 20 cm. What is the speed of the ball when it reaches the bottom of the cup? (Take $g = 10 m s^{- 2})$