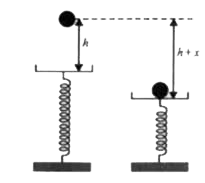
A ball of mass m is dropped from a heighth on a platform fixed at the top of a vertical spring, as shown in figure. The platform is depressed by a distance x. Then the spring constant is
mg(h+x)
mg(h+2x)
2mg(h+x)x2
mg(2h+x)
The correct Answer is:C
Loss in potential energy of the ball = mg(h+x)
Gain in elastic potential energy of the spring = 12kx2
According to the law of conservation of mechanical energy
mg(h+x)=12kx2 or k=2mg(h+x)x2 .
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (MOTIN IN A VERTICAL CIRCLE)
7 Videos
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (COLLISIONS)
35 Videos
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (POTENTIAL ENERGY AND CONSERVATIVE FORCES)
19 Videos
- THERMODYNAMICSBOOK - MTG GUIDECHAPTER - THERMODYNAMICSEXERCISE - AIPMT/NEET (MCQs)
26 Videos
Similar Questions
A ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View SolutionA ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View Solution
Knowledge Check
A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance d. The net work done in the process is
Amg(h+d)+12kd2Bmg(h+d)−12kd2Cmg(h−d)−12kd2Dmg(h−d)+12kd2A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance d. The net work done in the process is
Amg(h+d)+12kd2Bmg(h+d)−12kd2Cmg(h−d)−12kd2Dmg(h−d)+12kd2A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance d. The net work done in the process is
Amg(h+d)+12kd2Bmg(h+d)−12kd2Cmg(h−d)−12kd2Dmg(h−d)+12kd2
A particle of mass m=1kg is dropped from a height h=40cm on a light horizontal platform fixed to one end of an elastic spring, the other being fixed to a base, as shown in the diagram. The particle collides with the platform and sticks to it. As a result, the spring is compressed by an amount x=10cm. What is the force constant of the spring?
(Take g=10ms−2)
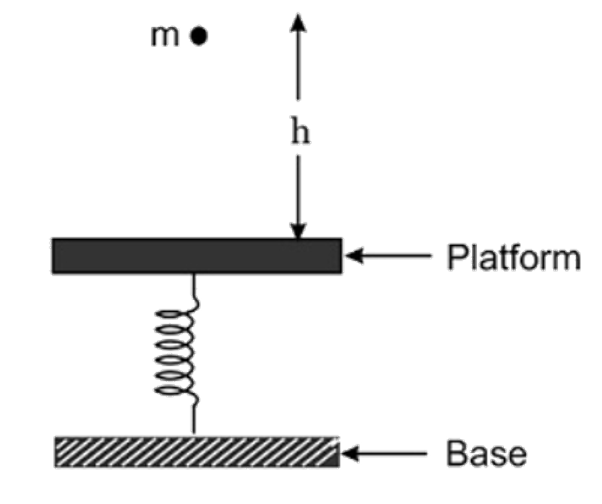
View SolutionA particle of mass m=1kg is dropped from a height h=40cm on a light horizontal platform fixed to one end of an elastic spring, the other being fixed to a base. The particle collides with the platform and sticks to it. As a result, the spring is compressed by an amount x=10cm. What is the force constant of the spring?
(Take g=10ms−2)

View SolutionA vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring , so that the spring is compressed by a distance d. The net work done in the process is
View SolutionA block of mass 2 kg initially at rest is dropped from a height of 1m into a vertical spring having force constant 490Nm−1. Calculate the maximum distance through which the spring will be compressed.
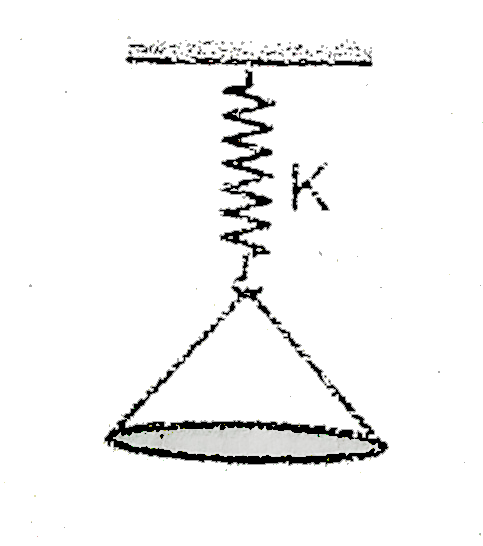
View SolutionA solid ball of mass m is made to fail from a height H on a pan suspended through a spring of spring constant K as shown in figure. If the does not rebound and the pan is massless, then amplitude of oscillation is
View Solution
