A particle is released from a height S. At certain height its kinetic energy is three times its potential energy. The height and speed of the particle at that instant are respectively
S4,3gS2
S4√3gSS
S2√3gSS
S4√3gSS
The correct Answer is:D
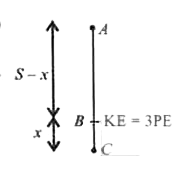
Velocity at B when dropped from A where AC = S.
v2=0+2g(S−x) ..(i)
or v2=2g(S−x)
potential energy at B=mgx
∴ Kinetic energy = 3×potential energy
∴12m×2g(S−x)=3×mgx
or S−x=3x or S=4x or x=S4
Putting this value of x in eqn. (i), we get
v2=2g(S−S4)=2g×3S4=3gS2 or v=√3gS2
Hence, x=S4 and v=√3gS2
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (MOTIN IN A VERTICAL CIRCLE)
7 Videos
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (COLLISIONS)
35 Videos
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (POTENTIAL ENERGY AND CONSERVATIVE FORCES)
19 Videos
- THERMODYNAMICSBOOK - MTG GUIDECHAPTER - THERMODYNAMICSEXERCISE - AIPMT/NEET (MCQs)
26 Videos
Similar Questions
A particle is released from height H. At certain height from the ground its kinetic energy is twice its gravitational potential energy. Find the height and speed of particle at that height.
View SolutionA particle is released from height H. At cartain height from the ground its kinetic energy is twice its gravitational potential energy. Find the height and speed of particle at that height.
View Solution
Knowledge Check
A particle is released from a height h. At a certain height, its kinetic energy is two times its potential energy. Height and speed of the particle at that instant are
Ah3√2gh3Bh32√gh3C2h3√2gh3Dh3√2ghA particle is dropped from height H. At a point its kinetic energy is x times of its potential energy. Find the speed of the particle at that point -
A[2gxH]1/2B[2g(x+1)Hx]1/2C[2gH(x+1)]1/2D[2gxH(x+1)]1/2A particle is realesed from a height H from ground. At certain height its kinetic energy is three times its gravitational potential energy with respect to ground. Then choose the correct option(s). (Given 'g' is acceleration due to gravity is constant).
AThe height of the particle at that instant is H2BThe height of the particle at that instant is H4CThe speed of the particle at that instant is √3gH2DThe speed of the particle at that instant is √3gH2
A particle is released from height S from the surface of the earth. At a certain height its KE is three times its PE. The height from the surface of earth and the speed of the particle at that instant are resp.
View SolutionKinetic energy of a particle on the surface is E0 and potential energy is−E02.
(a) Will the particle escape to infinity ?
(b) At some height its kinetic energy becomes 0.6E0. What is potential energy at this height ?
(c) If the particle escape to infinity , what is kinetic energy of the particle at infinity ?
View SolutionKinetic energy of a particle on the surface is e0 and potential energy is−E02.
(a) Will the particle escape to infinity ?
(b) At some height some height its kinetic energy becomes 0.6E0. What is potential energy at this height ?
(c) If the particle escape to infinity , what is kinetic energy of the particle at infinity ?
View SolutionA ball is released from certain height. It loses 50% of its kinetic energy on striking the ground. It will attain a height again equal to
View SolutionA particle is performing linear S.H.M. at a point A, on the path, its potential energy is three times kinetic energy. At another point B on the same path, its kinetic energy is 3 times the potential energy. The ratio of the potential energy at A to its potential energy at B is
View Solution
