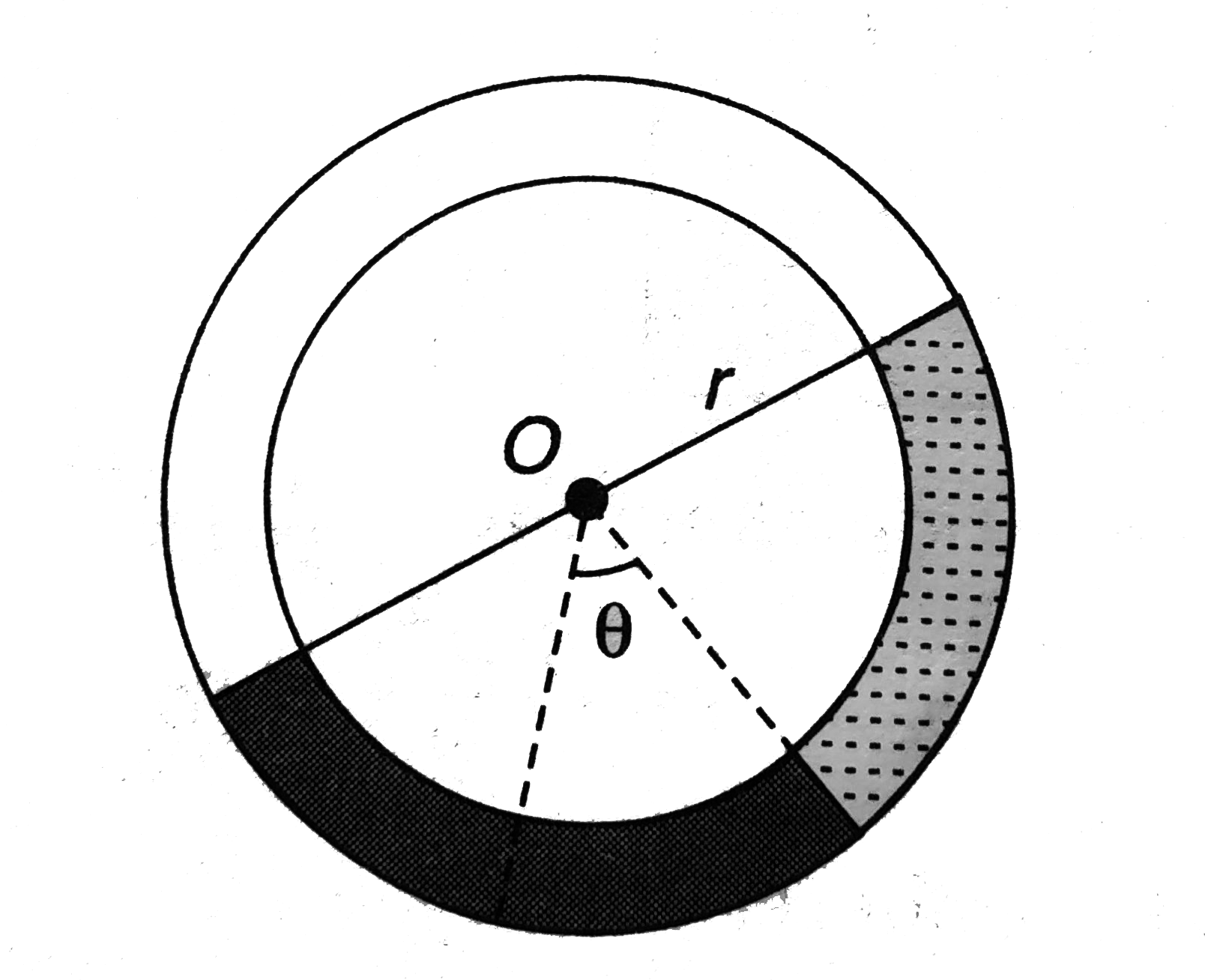
A uniform long tube is bent into a circle of radius R and it lies in a vertical plane. Two liquids of same volume but densities ρ and δ fill half the tube. The angle θ is
 Solution in Bengali
Solution in Bengali
tan−1(ρ−δρ−δ)
tan−1ρ/δ
tan−1δ/ρ
tan−1ρ+δρ−δ
Step by step video & image solution for A uniform long tube is bent into a circle of radius R and it lies in a vertical plane. Two liquids of same volume but densities rho and delta fill half the tube. The angle theta is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
→Aand→B are two vectors given by →A=2ˆi+3ˆjand→B=ˆi+ˆj. The magnitude of the component of →A along →B is
View SolutionGiven →A=2ˆi+3ˆjand→B=ˆi+ˆj . The component of vector →A along vector →B is
View SolutionA small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
View SolutionA thin uniform circular tube is kept in a vertical plane. Equal volume of two immiscible liquids whose densites are ρ1 and ρ2 fill half of the tube as shown. In equilibrium the radius passing through the interface makes an angle of 30∘ with vertical. The ratio of densities (ρ1/ρ2) is equal to

View SolutionWhen one end of a tube of radius r is immersed vertically in a liquid of density rho , surface tension S, the rise of liquid in the tube is h and angle of contact is theta . If the tube is broken and its length is made h' (lt h) , then find the value of height of rise of liquid in the tube and angle of contact.
View SolutionA tube in vertical plane is shown in figure. It is filled with a liquid of density rho and its end B is closed. Then the force exerted by the fluid on the tube at end B will be : [Neglect atmospheric pressure and assume the radius of the tube to be negligible in comparison to l ]
View SolutionA vertical U-tube has one of the its arms bent at θ from the vertical and then filled with a liquid of density ρ up to a height h in the vertical arm. Calculate the period of oscillations of the liquid when disturbed a little and released.
View SolutionA uniform long tube is bent into a circle of radius R and it lies in vertical plane. Two liquids of same volume but densities ρ and δ fill half the tube. The angle θ is

View SolutionA test tube of uniform cross-section is floated vertically in a liquid 'A' (density ρA) upto a mark on it when it is filled with 'x' ml of a liquid 'B' (density ρB). To make the test tube float in liquid B upto the same mark it is filled with y ml of the liquid A. Find the mass of the test tube.
View SolutionA thin uniform tube is bent into a circle of radius r in the vertical plane. Equal volumes of two immiscible liquids, whose densities are rho_(1) and rho_(2) (rho_(1) gt rho_(2)) fill half the circle. The angle theta between the radius vector passing though the common interface and the vertical is :
View SolutionThe height of liquid column in capillary tube is h the radius of capillary tube is r. rho is the density of liquid , g is acceleration due to gravity and theta is angle of contact . The surface tension of the liquid is ,
View SolutionThe radius of the bore of a capillary tube is r and the angle of contact of the liquid is theta . When the tube is dipped in the liquid , the radius of curvature of the meniscus of liquid rising in the tube is
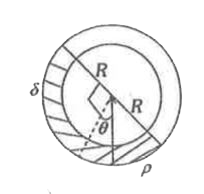
View Solutionएक समरूप लम्बी नलिका को R त्रिज्या के वृत्त में मोड़ा जाता है तथा यह ऊर्ध्वाधर तल में स्थित है। समान आयतन किन्तु घनत्व ρ तथा δ के दो द्रव आधी नलिका में भरे जाते है। तब कोण θ होगा-
View SolutionThe radius of the bore of a capillary tube is r and the angle of contact of the liquid is theta . When the tube is dipped in the liquid , the radius of curvature of the meniscus of liquid rising in the tube is
View SolutionA small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities are rho and sigma(rhogtsigma) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
View Solution
