A uniform long tube is bent into a circle of radius R and it lies in vertical plane. Two liquids of same volume but densities ρ and δ fill half the tube. The angle θ is

tan−1(ρ−δρ+δ)
tan−1(ρδ)
tan−1(δρ)
tan−1(ρ+δρ−δ)
The correct Answer is:A
From the figure, we have
δgR(cosθ+sinθ)=ρgR(cosθ−sinθ)
⇒δcosθ+δsinθ=ρcosθ−ρsinθ
⇒sinθ(δ+ρ)=cosθ(ρ−δ)⇒tanθ=ρ−δρ+δ
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
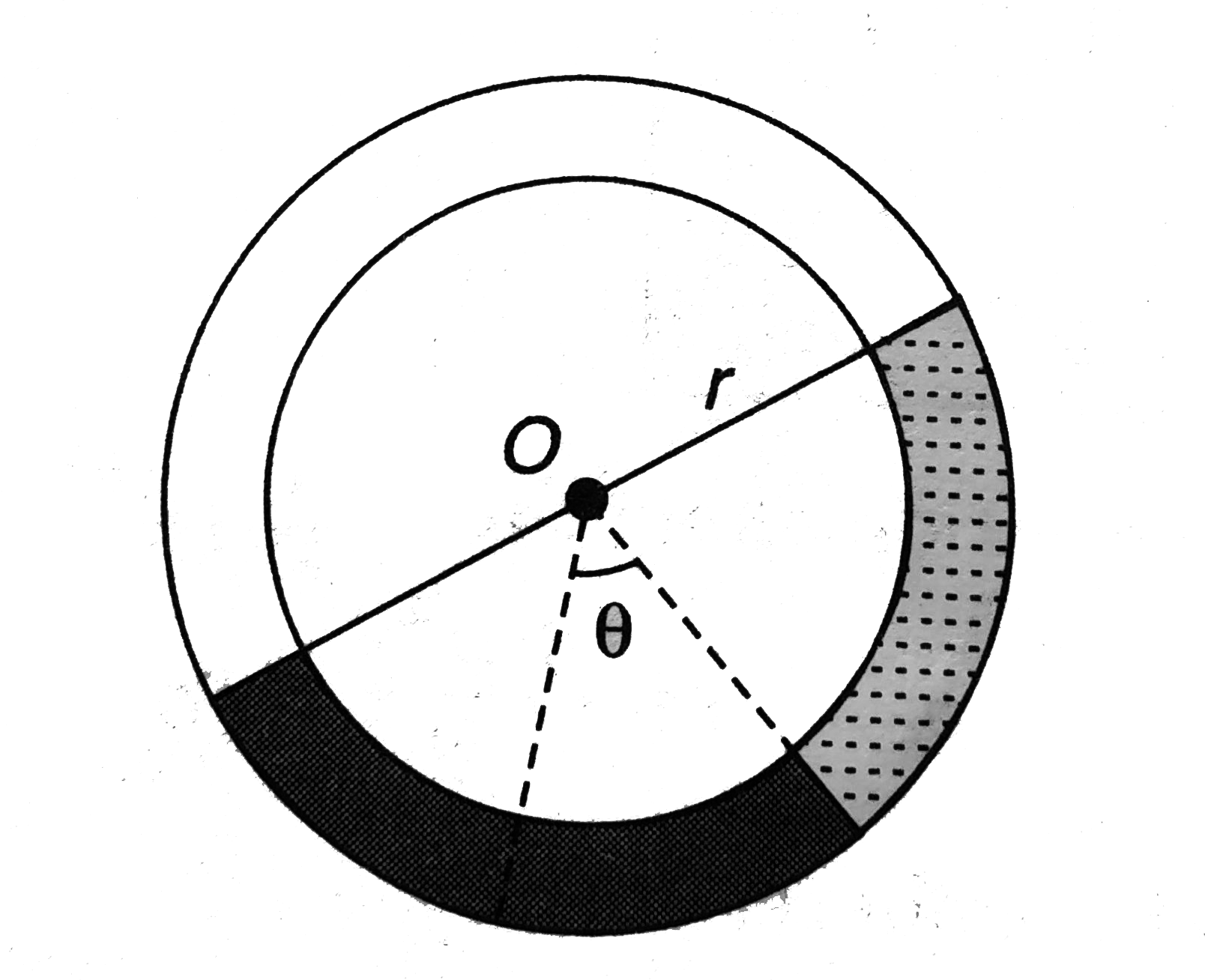
A small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
View SolutionIf two liquids of same volume but different densities ρ1 and ρ2 are mixed, then the density of the mixture is:
View SolutionA thin uniform circular tube is kept in a vertical plane. Equal volume of two immiscible liquids whose densites are ρ1 and ρ2 fill half of the tube as shown. In equilibrium the radius passing through the interface makes an angle of 30∘ with vertical. The ratio of densities (ρ1/ρ2) is equal to

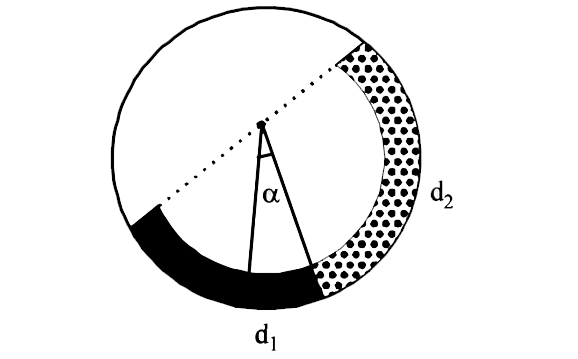
View SolutionThere is a circular tube in a vertical plane. Two liquids which do not mix and of densities d1andd2 are filled in the tube. Each liquid subtends 90∘ angle at centre. Radius joining their interface make an angle α with vertical. Ratio d1d2 is :
View SolutionTwo non - viscous, incompressible and immiscible liquids of densities (rho) and (1.5 rho) are poured into the two limbs of a circular tube of radius ( R) and small cross section kept fixed in a vertical plane as shown in fig. Each liquid occupies one fourth the cirumference of the tube.
Find the angle (theta) that the radius to the interface makes with the verticles in equilibrium position.
View SolutionA uniform rod of mass 2M is bent into four adjacent semicircles each of radius r, all lying in the same plane. The moment of inertia of the bent rod about an axis through one end A and perpendicular to plane of rod is

View SolutionA tube of radius r and sufficient height is dipped in a liquid of surface tension S and density ρ. Heat developed upto steady state will be
Note: θ is the contact angle
View SolutionA capillary tube with inner cross-section in the form of a square of side a is dipped vertically in a liquid of density ρ and surface tension ρ which wet the surface of capillary tube with angle of contact θ . The approximate height to which liquid will be raised in the tube is : (Neglect the effect of surface tension at the corners of capillary tube)
View SolutionA horizontal tube of uniform cross-sectional area A is bent in the form of U as shown in figure. If the liquid of density ρ enters and leaves the tube with velcity v, then the extermal force F requried to hold the bend stationary is

View Solution
An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-
View Solution
