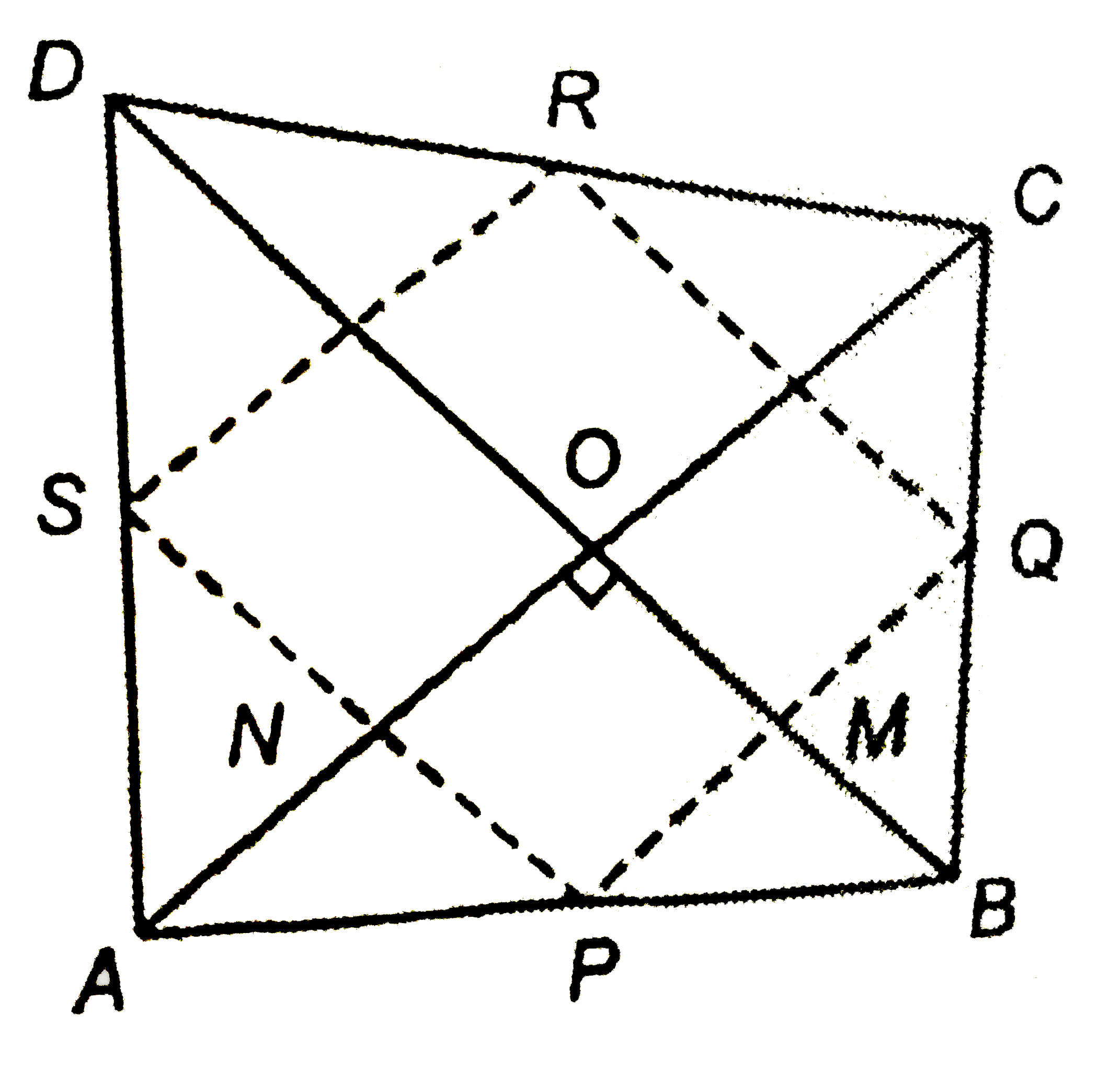
Prove that the figure formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
Step by step video & image solution for Prove that the figure formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram, so formed will be half of the area of the given quadrilateral (figure).

View SolutionIf the mid-points of the sides of a quadrilateral are joined in sequence, then prove that the area of the parallelogram so formed is half of the area of the given quadrilateral.
View Solutionसिद्ध कीजिए कि किसी चतुर्भुज कि क्रमागत भुजाओं के मध्य-बिंदुओं को मिलाने से बना चतुर्भुज समान्तर चतुर्भुज होता है।
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionProve by vector method that the lines joining the mid points of consecutive sides of a quadrilateral is a parallelogram.
View SolutionProve that the quadrilatral formed by joining the mid points of the sides of a quadrilateral is a parallelogram.
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
View Solution
