ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24cm2, then ar (ABC) = 24cm2.
Step by step video & image solution for ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm^2, then ar (ABC) = 24 cm^2. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
For parallelogram ABCD, ar(ABCD)=48 cm2 . Then ar(ABC)=___ cm2
View SolutionIn figure, ABCD and EFGD are two parallelograms and G is the mid-point of side CD. Then, ar (DPC) = (1)/(2) ar(EFGD).
View SolutionIn the given fig.
 ABCD is a parallelogram and ABE is a triangle. Also AB∣∣CE. If ar (ABCD) = 60cm2 then ar (ΔABE) is :
ABCD is a parallelogram and ABE is a triangle. Also AB∣∣CE. If ar (ABCD) = 60cm2 then ar (ΔABE) is :
View SolutionABCD is a parallelogram. If ar (ABC) = 18 cm2, then are (ABCD) = …………….. cm2
View SolutionIn the given figure, ABCD and ABFE are parallelograms such that ar(quad. EABC) =19 cm2 and ar(||gm ABCD) = 28 cm2. Then, ar(△BCF) is
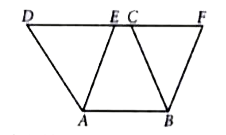
View SolutionIn the figure ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar(DPC) = 1/2 ar(EFGD)
View SolutionABCD is a parallelogram. P is any point on CD. If ar(triangleDPA) = 15 cm^2 and ar(triangleAPC) = 20 cm^2 , the ar (triangleAPB) =
View Solution
