In three dimensions there may be more than one point, which are equidistant from three given noncolliner points A,B,C. One of these points will be circumcentre of the triangle ABC
The y coordinate of orthocentre of the triangle ABC
A
B
C
D
Text Solution
The correct Answer is:a
|
Topper's Solved these Questions
- 3D COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 3D COORDINATE SYSTEMEXERCISE - LECTURE SHEET (EXERCISE-I) (Integer Type Questions)
3 Videos
- 3D COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 3D COORDINATE SYSTEMEXERCISE - PRACTICE SHEET (EXERCISE-I) (LEVEL-I) (Straight Objective Type Questions)
22 Videos
- 3D COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 3D COORDINATE SYSTEMEXERCISE - LECTURE SHEET (EXERCISE-I) (Straight Objective Type Questions) (Matrix Matching Type Questions)
1 Videos
- 2D-COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 2D-COORDINATE SYSTEMEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
14 Videos
- 3D-COORDINATE SYSTEMBOOK - AAKASH SERIESCHAPTER - 3D-COORDINATE SYSTEMEXERCISE - PRACTICE EXERCISE
40 Videos
Similar Questions
Knowledge Check
In three dimensions there may be more than one point, which are equidistant from three given non-collinear points A, B, C. One of these points will be circumcentre of the triangle ABC.
The y-coordinate of orthocenter of the triangle ABC.A3a2c2−a2b2−b2c2a2b2+b2c2+c2a2.bBab+b2−aca+b+cCb−2(a2c2+b4)a3+b3+c3Dnone of theseIn three dimensions there may be more than one point, which are equidistant from three given non-collinear points A, B, C. One of these points will be circumcentre of the triangle ABC.
The y-coordinate of the circumcentre of triangle ABC must beAaca+b+cBa2c2−b4a3+b3+c3Cb2c2+a2b2−a2c2a2b2+b2c2+c2a2.bDnone of theseThe plane 2x+y+2z=9 intersects the coordinate axes at A,B,C.The orthocentre of the triangle ABC is
A(2,1,2)B(32,3,32)C(313,113,313)D(97,277,97)
Find the coordinates of the point equidistant from three given points A(5,1),B(−3,−7) and C(7,−1).
View SolutionPoints A(3,5),B(−1,4)andC(7,−6) are the vertices of Δ ABC. Find the coordinates of the centroid of the triangle
View SolutionThe coordinates of the point which is equidistant from the three vertices of the △AOB as shown in the figure is
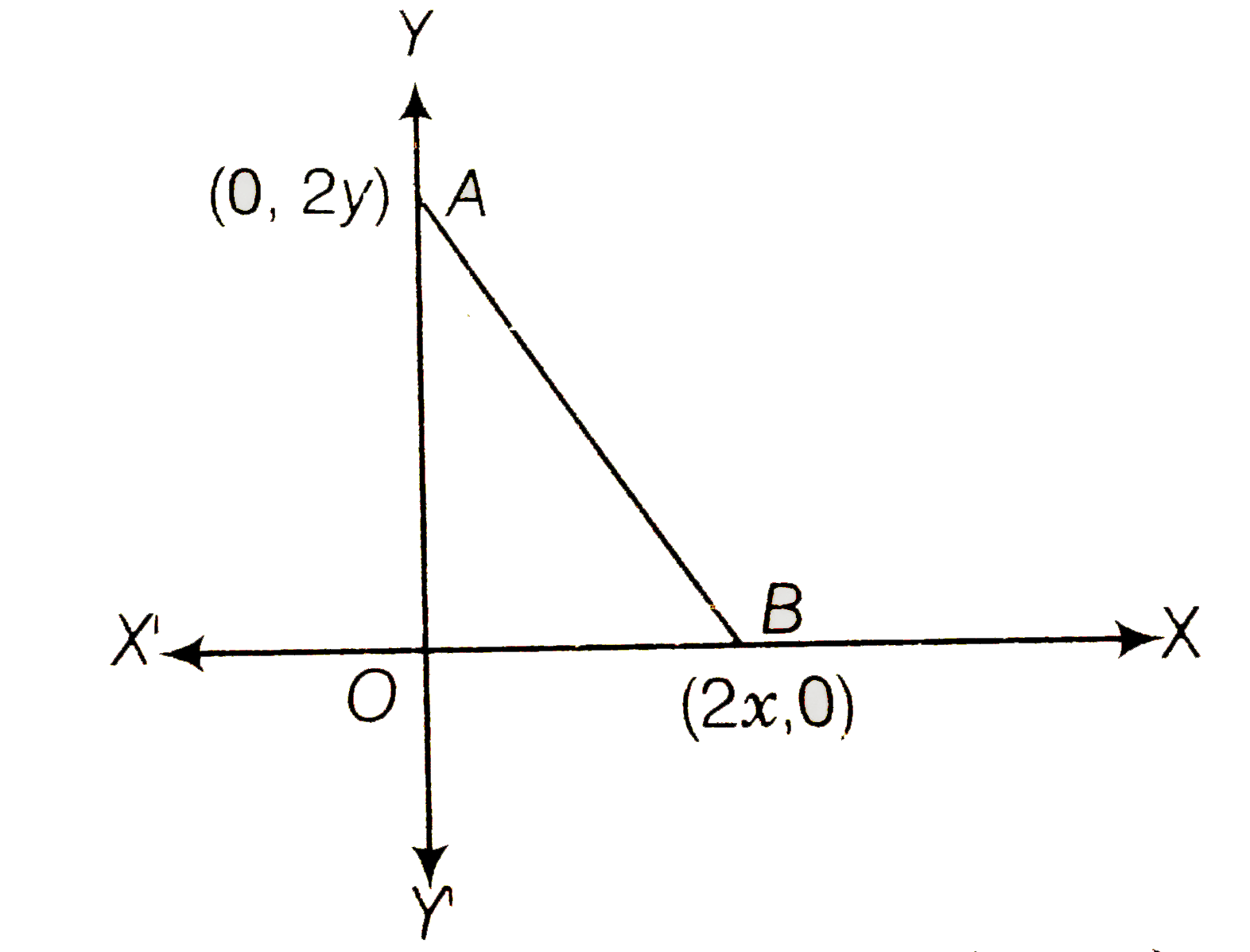
View SolutionThe coordinates of the point which is equidistant from the three vertices of the △AOB as shown in the figure is

View SolutionWhat is the number of points in the plane of a triangle ABC which are at equal distance from the vertices of the triangle ?
View Solution
