A heavy particle hanging from a string of length l is projected horizontally with speed √gl. Find the speed of the particle at the point where the tension in the string equals weight of the particle.
√gI3
√gI2
√(3gI)
√2gI
Step by step video & image solution for A heavy particle hanging from a string of length l is projected horizontally with speed sqrtgl. Find the speed of the particle at the point where the tension in the string equals weight of the particle. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View SolutionA heavy particle hangs from a point O, by a string of length a. It is projected horizontally with a velocity u=√(2+√3)ag . The angle with the downward vertical, string makes where string becomes slack is :
View Solution
Knowledge Check
A stone hanging from a massless string of length 15m is projected horizontally with speed √147ms−1 Then the Speed of the particle, at the point where tension in string equals the weight of particle, is
A10ms−1B7ms−1C12ms−1Dnone of theseA stone hanging from a massless string of length 15m is projected horizontally with speed √147ms−1 Then the Speed of the particle, at the point where tension in string equals the weight of particle, is
A10ms−1B7ms−1C12ms−1Dnone of theseA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
A√31g,cos−1(3/2)B√1g3,cos−1(2/3)C√3g3,cos−1(2/3)D√gl3,cos−1(2/3)
A particle is suspended by a light vertical inelastic string of length 1 from a fixed support. At its equilbrium position it is projected horizontally with a speed √6gl. Find the ratio of the tension in the string in its horizontal position to that in the string when the particle is vertically above the point of support.
View SolutionA particle hanging from a thread is launched horizontally with small speed that it does not even reach to the horizontal level. Is the motion periodic or oscillatory?
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View SolutionThe bob hanging from a light string is projected horizontally with a speed u0. In the subsequent upward motion of the bob in vertically plane
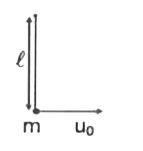
View SolutionA particle of mass ma is suspended from a ceiling thrugh a string of length L. The prticle moves in a horizontal circle of radius r. Find (a) the speed of the prticle and (b). the tension in the string. Sch a system is called a conical pendulum
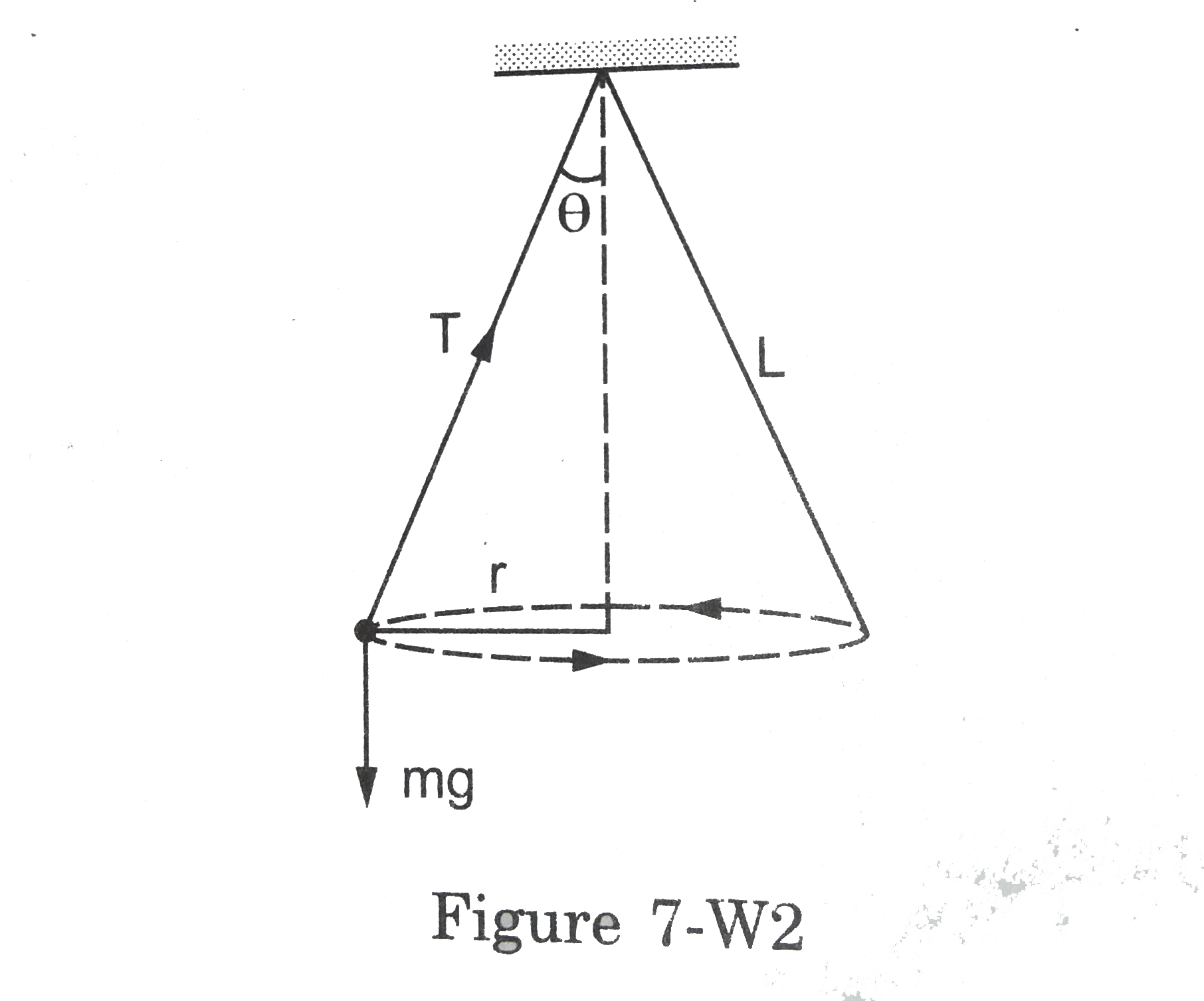
.
View Solution
