Question

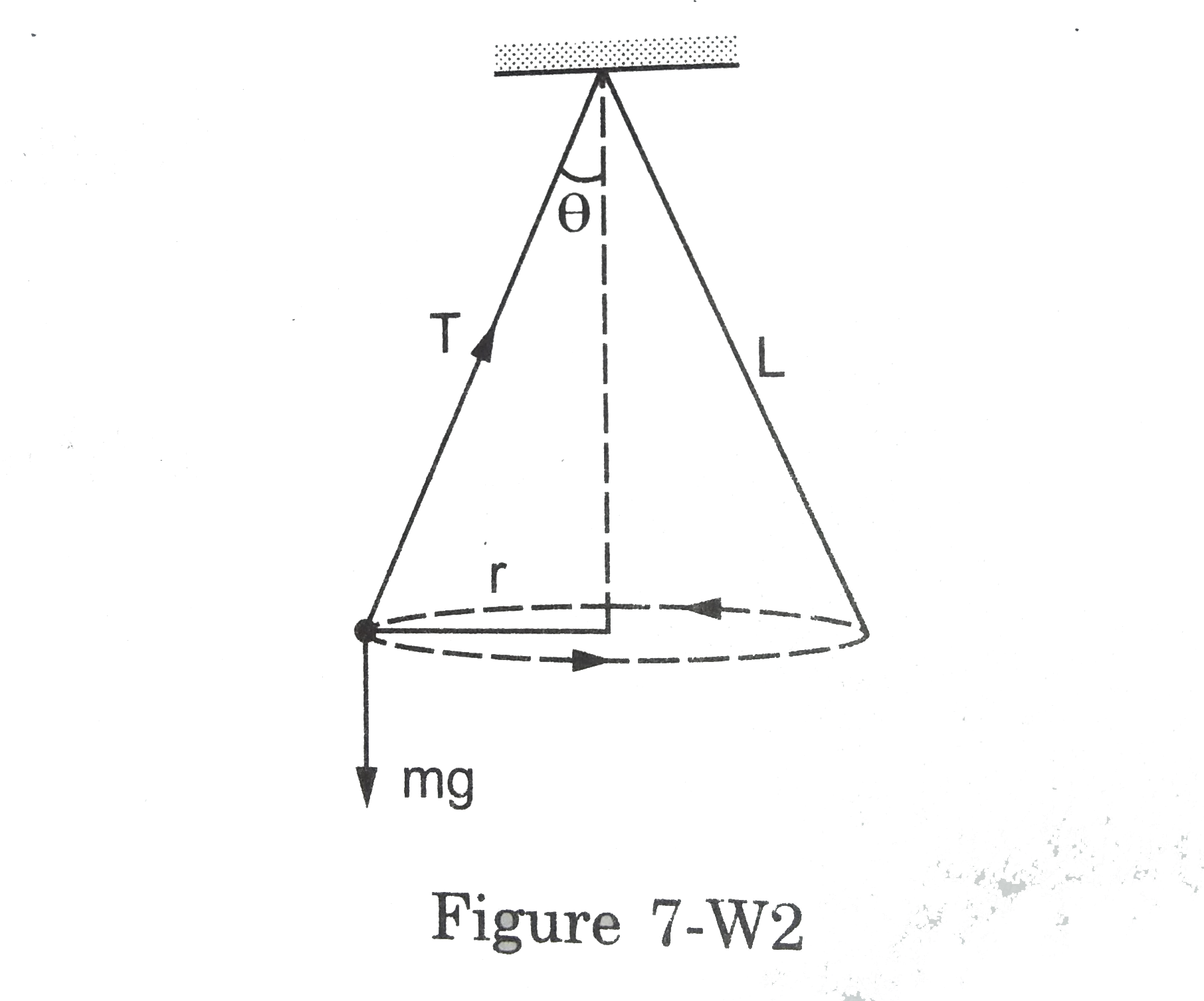
A particle of mass ma is suspended from a ceiling thrugh a string of length $L$. The prticle moves in a horizontal circle of radius $r$. Find $\left(a\right)$ the speed of the prticle and $\left(b\right)$. the tension in the string. Sch a system is called a conical pendulum

.

Options

A. `v=(rsqrtg)/((L^2-r^2)^(1/4)) and T=(mgL)/((L^2-r^2)^(1/2))`
B. `v=(r^2sqrtg)/((L^3-r^3)^(1/4)) and T=(mgL)/((L^2-r^2)^(1/2))`
C. `v=(rsqrtg)/((L^2-r^2)^(1/4)) and T=(mgL^2)/((L^2-r^2)^(1/2))`
D. `v=(rsqrtg)/((L^2-r^2)^(1/4)) and T=(mgL)/((L^2-r^2)^(1/4))`

Answer

A

Explanation

The situation shown in ure. The angle `theta` made by the string with verticla is given by
`sintheta=r/L`………..i

The forces on the pasrticle are
a. the tension T along the string and
b. the weight mg vertically downward.
The particle is moving in a circle with a constant speed v. Thus, the radial acceleration towards the centre has magnitude `v^2/h`. Resolving the forces along the radia direction and applying Newton's second law,
`Tsintheta=m(v^2/r)` ..........ii
As thee is no cceleration in vertical directin we have from Newton's first law
`Tcostheta=mg`...............iii
Dividing ii by iii,
`tantheta=v^2/(rg)`
`or, v=sqrt(rg tantheta)`
and from iii,
`T=(mg)/(costheta)`
using i.
`v=(rsqrtg)/((L^2-r^2)^(1/4)) and T=(mgL)/((L^2-r^2)^(1/2))`