A man pulls out a block of mass m from the depth d with help of a light string. If acceleration of the block is then the work done by the string on the block will be
The correct Answer is:D
To solve the problem of finding the work done by the string on the block, we can follow these steps:
1. Identify the Forces Acting on the Block:
The block of mass m is subjected to two main forces:
- The gravitational force acting downward: Fg=mg
- The tension in the string acting upward: T
2. Apply Newton's Second Law:
According to Newton's second law, the net force acting on the block is equal to the mass of the block multiplied by its acceleration. The block is accelerating upwards with an acceleration of g2. Therefore, we can write the equation:
T−mg=ma
where a=g2.
3. Substitute the Values:
Substituting a into the equation gives:
T−mg=m(g2)
4. Rearranging the Equation:
Rearranging the equation to solve for T:
T=mg+m(g2)
T=mg+mg2
T=2mg2+mg2=3mg2
5. Calculate the Work Done by the String:
The work done W by the tension in the string as the block is pulled out from depth d is given by the formula:
W=T⋅d
Substituting the value of T:
W=(3mg2)⋅d
W=3mgd2
Final Answer:
The work done by the string on the block is 3mgd2.
---
The block of mass m is subjected to two main forces:
- The gravitational force acting downward: Fg=mg
- The tension in the string acting upward: T
According to Newton's second law, the net force acting on the block is equal to the mass of the block multiplied by its acceleration. The block is accelerating upwards with an acceleration of g2. Therefore, we can write the equation:
T−mg=ma
where a=g2.
Substituting a into the equation gives:
T−mg=m(g2)
Rearranging the equation to solve for T:
T=mg+m(g2)
T=mg+mg2
T=2mg2+mg2=3mg2
The work done W by the tension in the string as the block is pulled out from depth d is given by the formula:
W=T⋅d
Substituting the value of T:
W=(3mg2)⋅d
W=3mgd2
The work done by the string on the block is 3mgd2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A body of mass m is allowed to fall with the help of string with downward acceleration g/6 to distance x. The work done by the string is
Amgx6B−mgx6C5mgx6D−5mgx6A mass M is lowered with the help of a string by a distance h at a distance acceleration g/2. The work done by the string will be
A(a) Mgh2B(b) −Mgh2C(c) 3Mgh2D(d) −3Mgh2A body of mass m is allowed to fall with the help of string with downward acceleration g6 to a distance x. The work done by the string is
Amgx6B−mgx6C5mgx6D−5mgx6
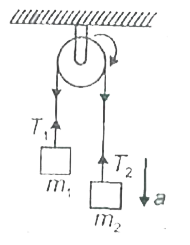
Figure shows a pulley of mass m and radius r with two blocks of masses m1 and m2 attached with a light and unstretchable string. Find the acceleration of the blocks, tensions in the string and the force exerted by the pulley on the celling from which it is hanging. Assume no slipping between the string and the wheel.
View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
View SolutionA cord is used to lower vertically a block of mass M, a distance d at a constant downward acceleration of g4, then the work done by the cord on the block is
View SolutionThe block of mass m is at rest. Find the tension in the string A .

View SolutionA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a find the force applied by the string and by the table N on the block.

View Solution

