A rope of length 5 m has uniform mass per unit length. λ=2kgm The rope is pulled by a constant force of 10N on the smooth horizontal surface as shown in figure The tension in the rope at x = 2 m from polit A is
2 N
8 N
6 N
5 N
The correct Answer is:D
To find the tension in the rope at a point 2 m from point A, we can follow these steps:
Step 1: Identify the mass of the rope
The mass per unit length (λ) of the rope is given as 2 kg/m. The total length of the rope is 5 m. Therefore, the total mass (M) of the rope can be calculated as:
M=λ×length=2kg/m×5m=10kg
Step 2: Calculate the acceleration of the rope
The rope is subjected to a constant force (F) of 10 N. Using Newton's second law, we can find the acceleration (a) of the entire rope:
F=M⋅a
Rearranging gives:
a=FM=10N10kg=1m/s2
Step 3: Determine the mass of the segment of the rope
We need to find the tension at a point 2 m from point A. The mass of the segment of the rope from point A to this point (2 m) can be calculated as:
m=λ×length of segment=2kg/m×2m=4kg
Step 4: Calculate the net force acting on the segment
The net force (F_net) acting on the 2 m segment of the rope can be calculated using Newton's second law:
Fnet=m⋅a=4kg×1m/s2=4N
Step 5: Calculate the tension in the rope at 2 m
The tension (T) at the point 2 m from point A can be found by considering the forces acting on the segment. The tension at this point must balance the force needed to accelerate the 2 m segment:
T−Fpull=Fnet
Where Fpull is the force pulling the entire rope, which is 10 N. Rearranging gives:
T=Fnet+Fpull=4N+10N=14N
Final Answer
The tension in the rope at a point 2 m from point A is 14 N.
The mass per unit length (λ) of the rope is given as 2 kg/m. The total length of the rope is 5 m. Therefore, the total mass (M) of the rope can be calculated as:
M=λ×length=2kg/m×5m=10kg
The rope is subjected to a constant force (F) of 10 N. Using Newton's second law, we can find the acceleration (a) of the entire rope:
F=M⋅a
Rearranging gives:
a=FM=10N10kg=1m/s2
We need to find the tension at a point 2 m from point A. The mass of the segment of the rope from point A to this point (2 m) can be calculated as:
m=λ×length of segment=2kg/m×2m=4kg
The net force (F_net) acting on the 2 m segment of the rope can be calculated using Newton's second law:
Fnet=m⋅a=4kg×1m/s2=4N
The tension (T) at the point 2 m from point A can be found by considering the forces acting on the segment. The tension at this point must balance the force needed to accelerate the 2 m segment:
T−Fpull=Fnet
Where Fpull is the force pulling the entire rope, which is 10 N. Rearranging gives:
T=Fnet+Fpull=4N+10N=14N
The tension in the rope at a point 2 m from point A is 14 N.
Topper's Solved these Questions
Similar Questions
A uniform rope of length of length L is pulled by a force F on a smooth surface. Find tension in the rope at a distance x from the end where force is applied.
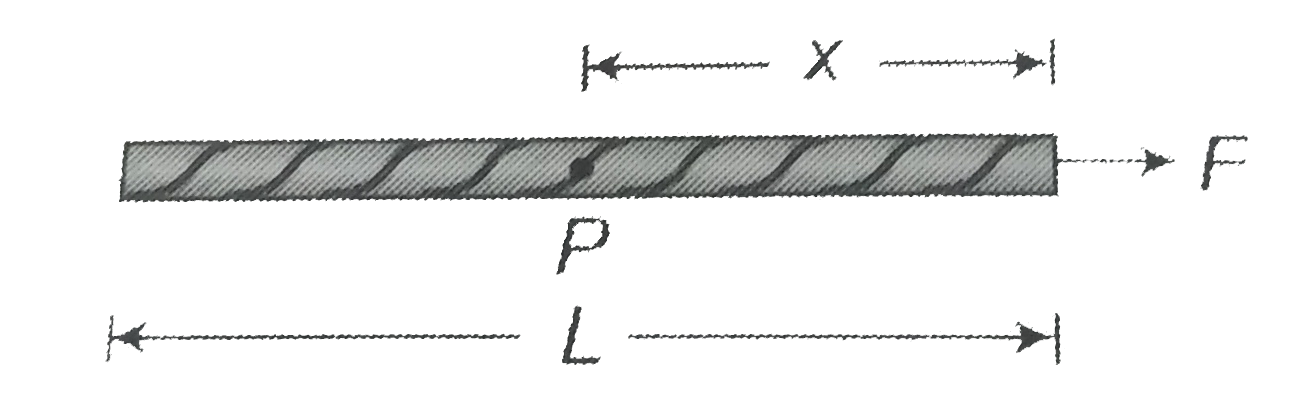
View SolutionA uniform rope of length L is pulled by a constant force F. What is the tension in the rope at a distance l from the end where it is applied?
View Solution
Knowledge Check
A rope of length L has its mass per unit langth λ varies according to the function λ(x)=ex/L. The rope is pulled by a constant force of 1 N on a smooth horizontal surface. The tension in the rope at x=L/2 is :
 A0.50 NB0.38 NC0.62 NDNone
A0.50 NB0.38 NC0.62 NDNoneA rope of length 10m and linear density 0.5kg/m is lying length wise on a smooth horizontal floor. It is pulled by a force of 25 N. The tension in the rope at a point 6m away from the point of application is
A20 NB15 NC10 ND5 NA rope of length 5 m is kept on frictionless surface and a force of 5 N is applied to one of its end. Find the tension in the rope at 1 m from this end
A1 NB3 NC4 ND5 N
A rope of length 15 m and linear density 2 kg/m is lying length wise on a horizontal smooth table. It is pulled by a force of 25 N. The tension in the rope at the point 7 m away from the point of application, will be -
View SolutionA uniform rope of length 10m is on a smooth horizontal surface. It is being pulled by a horizontal force of 20N at one end. The ratio of tension at a distance of 4m from force end to tension at a distance of 4m from free end is
View SolutionA block of mass M is attached to a uniform rope of mass m. This arrangement is pulled by applying a force F at the rope as shown. Find the tension in the rope (a) at the junction of the rope and the block (b) at the mid point of the rope.
View SolutionA rope of length 10m and linear density 0.5kg/m is lying length wise on a smooth horizontal floor It is pulled by a force of 25N. The tension in the rope at a point 6m away from the point of application is .
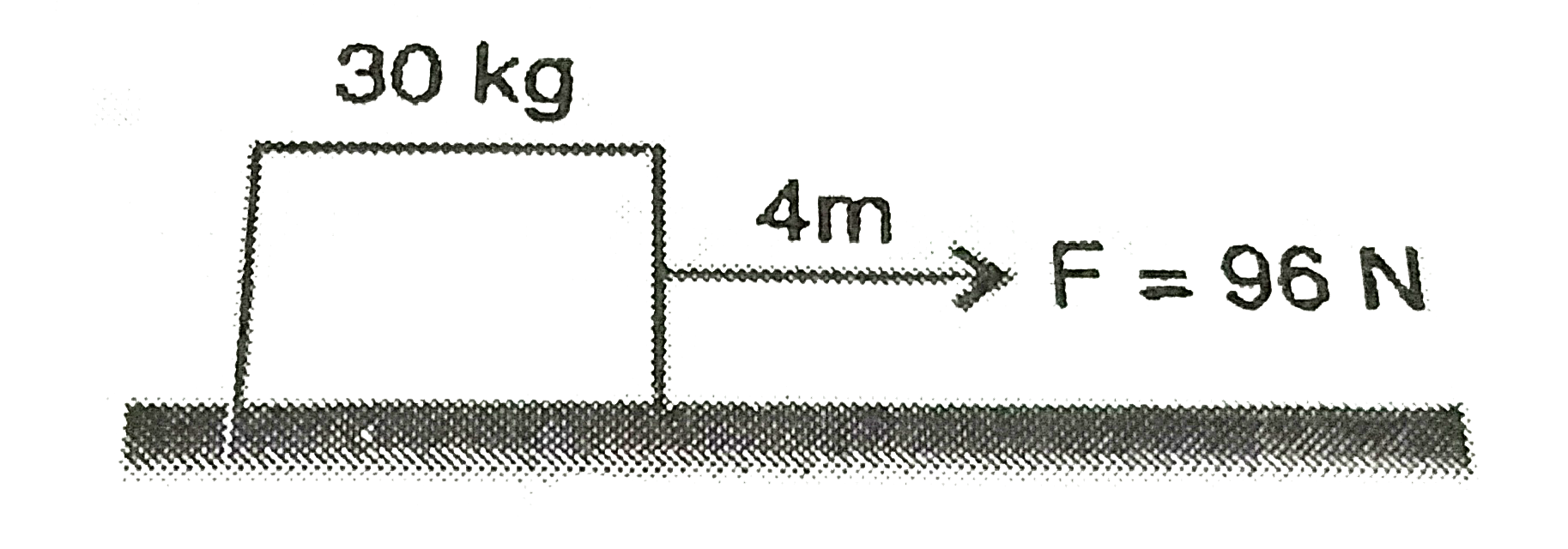
View SolutionA 30 kg body is pulled by a rope 4 m long on a frictionless horizontal surface by a force 96 N if mass of the rope is 2 kg, force acting on the body is:
View Solution
