A body of mass m hits a wall with speed v at an angle of 30o with normal and reflects at same angle from normal on other side of normal. The magnitude of change in linear momentum of the body is (Consider elastic collision)
8√3mv2
mv
√3mv
Zero
The correct Answer is:c
To solve the problem of finding the magnitude of change in linear momentum of a body of mass m that hits a wall at an angle of 30∘ with the normal and reflects elastically, we can follow these steps:
Step 1: Understand the Initial Conditions
The body hits the wall with speed v at an angle of 30∘ with respect to the normal. We need to resolve the velocity into its components.
Step 2: Resolve Initial Momentum
The initial momentum →pi can be resolved into two components:
- The component parallel to the wall (x-direction): pix=mvcos(30∘)
- The component perpendicular to the wall (y-direction): piy=−mvsin(30∘) (negative because it is directed towards the wall)
Using the values of cos(30∘)=√32 and sin(30∘)=12:
pix=mv⋅√32=mv√32
piy=−mv⋅12=−mv2
Thus, the initial momentum vector is:
→pi=(mv√32^i−mv2^j)
Step 3: Resolve Final Momentum
After the collision, the body reflects off the wall at the same angle, so:
- The x-component remains the same: pfx=−mvcos(30∘)=−mv√32
- The y-component changes direction: pfy=−(−mvsin(30∘))=mv2
Thus, the final momentum vector is:
→pf=(−mv√32^i+mv2^j)
Step 4: Calculate Change in Momentum
The change in momentum Δ→p is given by:
Δ→p=→pf−→pi
Substituting the values:
Δ→p=(−mv√32^i+mv2^j)−(mv√32^i−mv2^j)
=−mv√32^i+mv2^j−mv√32^i+mv2^j
=−mv√3^i+mv^j
Step 5: Find the Magnitude of Change in Momentum
The magnitude of the change in momentum is:
|Δ→p|=√(−mv√3)2+(mv)2
=√3m2v2+m2v2=√4m2v2=2mv
Final Answer
The magnitude of the change in linear momentum of the body is 2mv.
The body hits the wall with speed v at an angle of 30∘ with respect to the normal. We need to resolve the velocity into its components.
The initial momentum →pi can be resolved into two components:
- The component parallel to the wall (x-direction): pix=mvcos(30∘)
- The component perpendicular to the wall (y-direction): piy=−mvsin(30∘) (negative because it is directed towards the wall)
pix=mv⋅√32=mv√32
piy=−mv⋅12=−mv2
→pi=(mv√32^i−mv2^j)
After the collision, the body reflects off the wall at the same angle, so:
- The x-component remains the same: pfx=−mvcos(30∘)=−mv√32
- The y-component changes direction: pfy=−(−mvsin(30∘))=mv2
→pf=(−mv√32^i+mv2^j)
The change in momentum Δ→p is given by:
Δ→p=→pf−→pi
Substituting the values:
Δ→p=(−mv√32^i+mv2^j)−(mv√32^i−mv2^j)
=−mv√32^i+mv2^j−mv√32^i+mv2^j
=−mv√3^i+mv^j
The magnitude of the change in momentum is:
|Δ→p|=√(−mv√3)2+(mv)2
=√3m2v2+m2v2=√4m2v2=2mv
The magnitude of the change in linear momentum of the body is 2mv.
Topper's Solved these Questions
Similar Questions
A body of mass m hits a wall with speed v at an angle of 30degree with normal and reflects at same angle from normal on other side of normal. The magnitude of change in linear momentum of the body is (Consider elastic collision)
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
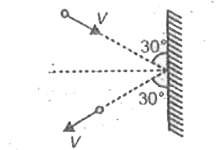
View Solution
Knowledge Check
A ball of mass 3 kg collides with a wall with velocity 10 m/sec at an angle of 30° and after collision reflects at the same angle with the same speed. The change in momentum of ball in MKS unit is-
A20B30C15D45A mass m with velocity u strikes a wall normally and returns with same speed. What is the magnitude of the change in momentum of the body when it returns.
A4 muBmuC2muDzeroA body of mass 0.5kg is projected under the gravity with a speed of 98m/s at an angle of 30∘ with the horizontal. The change in momentum (in magnitude) of the body when it strikes the ground is
A24.5 N-sB49.0 N-sC98.0 N-sD50.0 N-s
A body of mass m is projected with velocity v at an angle of 45∘ with the horizontal. Find the change in its momentum at the end of flight.
View SolutionAn object of m kg with speed of ms−1 strikes a wall at an angle θ and rebounds at the same speed and same angle. Find the magnitude of change in the momentum of object.
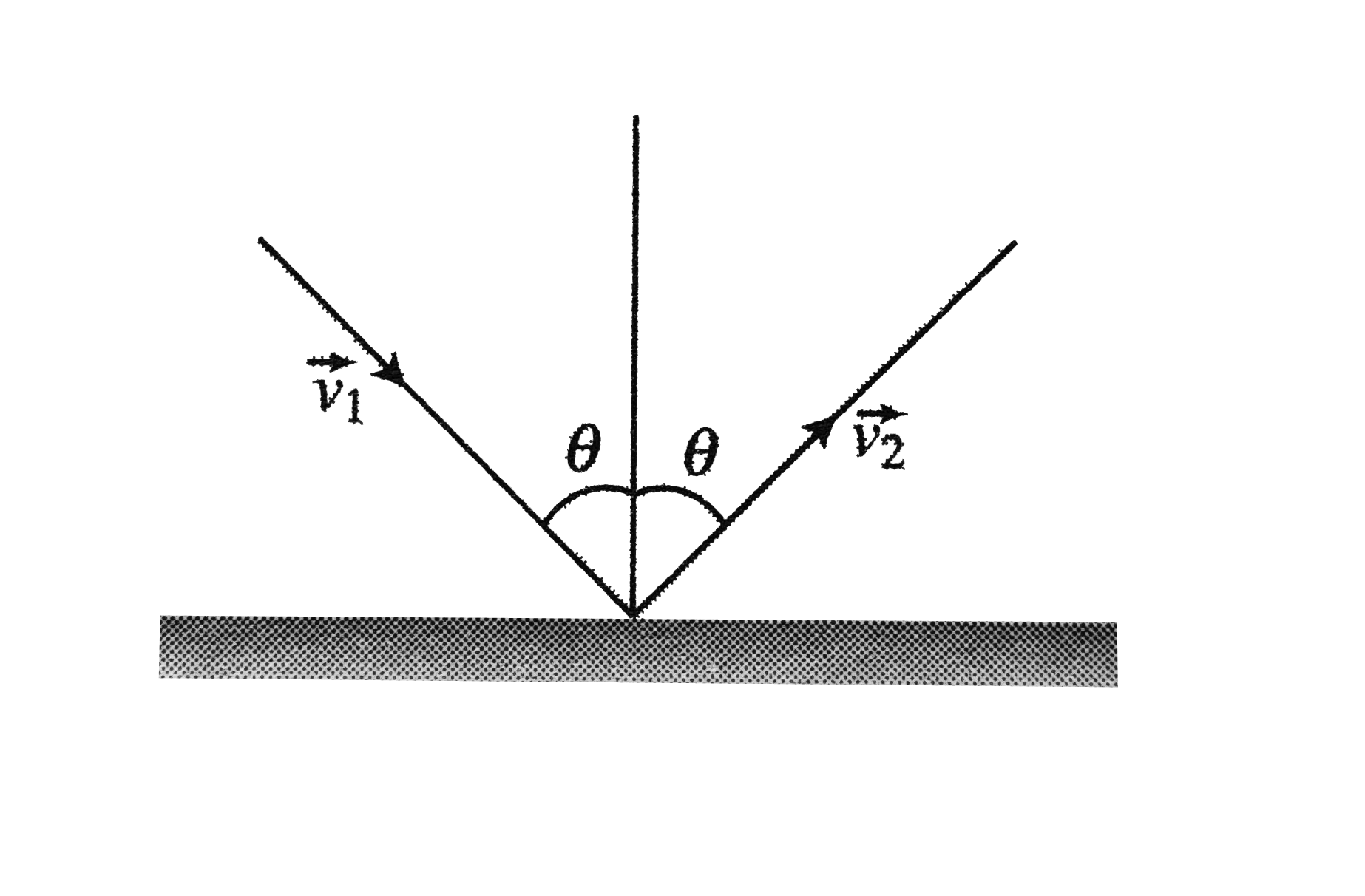
View SolutionA body of mass 3 kg hits a wall at an angle of 60∘ & returns at the same angle. The impact time was 0.2s. Calculate the force exerted on the wall:
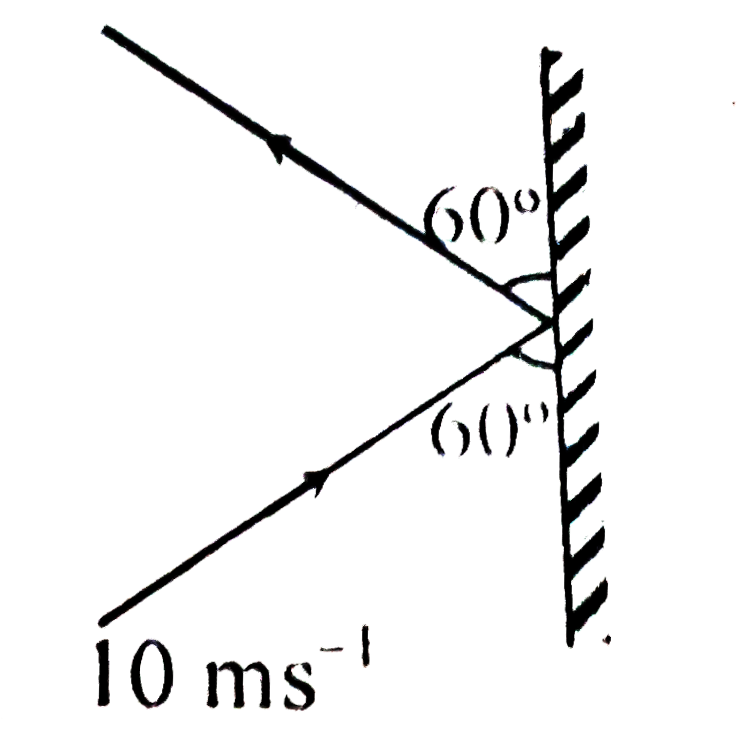
View SolutionA body of mass m is projected with intial speed u at an angle θ with the horizontal. The change in momentum of body after time t is :-
View SolutionA cricket ball of mass m strikes the bat with speed v normally and bounces back with speed v normally. The change in momentum of the ball is
View Solution
