Ratio of escape speeds from the surfaces of two uniformly uniformly dense planet of densities rho and 2ρ respectively having equal radii is
1√2
12
1
2
To find the ratio of escape speeds from the surfaces of two uniformly dense planets with densities ρ and 2ρ respectively, we can follow these steps:
Step 1: Understand the formula for escape speed
The escape speed ve from the surface of a planet is given by the formula:
ve=√2GMR
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
Step 2: Calculate the mass of the planets
The mass M of a planet can be expressed in terms of its density ρ and volume V:
M=ρV
For a sphere, the volume V is given by:
V=43πR3
Thus, the mass of the first planet (density ρ) is:
M1=ρ(43πR3)=43πρR3
And the mass of the second planet (density 2ρ) is:
M2=2ρ(43πR3)=83πρR3
Step 3: Substitute the masses into the escape speed formula
Now, we can substitute M1 and M2 into the escape speed formula for both planets.
For the first planet:
ve1=√2GM1R=
⎷2G(43πρR3)R=√8πGρR23
For the second planet:
ve2=√2GM2R=
⎷2G(83πρR3)R=√16πGρR23
Step 4: Calculate the ratio of escape speeds
Now, we can find the ratio of the escape speeds ve1ve2:
ve1ve2=√8πGρR23√16πGρR23
This simplifies to:
ve1ve2=√8√16=2√24=√22
Final Answer
Thus, the ratio of escape speeds from the surfaces of the two planets is:
ve1ve2=√22
The escape speed ve from the surface of a planet is given by the formula:
ve=√2GMR
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
The mass M of a planet can be expressed in terms of its density ρ and volume V:
M=ρV
For a sphere, the volume V is given by:
V=43πR3
Thus, the mass of the first planet (density ρ) is:
M1=ρ(43πR3)=43πρR3
And the mass of the second planet (density 2ρ) is:
M2=2ρ(43πR3)=83πρR3
Now, we can substitute M1 and M2 into the escape speed formula for both planets.
ve1=√2GM1R=
⎷2G(43πρR3)R=√8πGρR23
ve2=√2GM2R=
⎷2G(83πρR3)R=√16πGρR23
Now, we can find the ratio of the escape speeds ve1ve2:
ve1ve2=√8πGρR23√16πGρR23
This simplifies to:
ve1ve2=√8√16=2√24=√22
Thus, the ratio of escape speeds from the surfaces of the two planets is:
ve1ve2=√22
Topper's Solved these Questions
Similar Questions
Show that the escape velocity of an object from the speeds of two planets of masses 2M and 3M and radii 2R and R respectively.
View SolutionTwo solid sphere (A and B) are made of metals of different densities ρA and ρB respectively. If their masses are equal, the ratio of their moments of inertia (IAIB) about their respective diameter is
View Solution
Knowledge Check
The escape velocity from the surface of the earth of radius R and density ρ
A2R√2πρG3B2√2πρG3C2π√RgD√2πGρR2A solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densityes ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
A(rho-rho_(1))/(rho_(2)-rho)Bρ2−ρρ−ρ1C(rho+rho_(1))/(rho+rho_(2))D(rho+rho_(2))/(rho+rho_(1))If two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
Aρ=ρ1+ρ22Bρ=ρ1+ρ22ρ1ρ2Cρ=2ρ1ρ2ρ1+ρ2Dρ=ρ1ρ2ρ1+ρ2
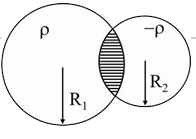
Two non-conducting spheres of radii R1 and R2 and carrying uniform volume charge densities +ρ and −ρ respectively are placed such that they partially overlapping region.
View SolutionWeight of a body on the surfaces of two planets is the same. If their densities are d1andd2, then ratio of their radii is
View SolutionSelect and write the corrcet answer :
The escape speed of a body from the surface of a planet of density ρ and radius R is proportional to
View SolutionThe radii of a planet and its satellite are 2r and r and their densities are ρ and 2ρ respectively. Their centres are separated by a distance d. The minimum speed with which a body should be projected from the mid point of the line joining their centres so that the body escapes to infinity is (G-universal gravitational constant)
View SolutionPertaining to two planets, the ratio of escape velocities from respective surfaces is 1:2 , the ratio of the time period of the same simple pendulum at their respective surfaces is 2:1 (in same order). Then the ratio of their average densities is
View Solution
