The velocities of our molecules are V, 2V, 4V and √2V, respectively. Their r.m.s. speed is
2.4v
2.2 v
24 v
0.2 v
To calculate the root mean square (r.m.s.) speed of the molecules with velocities V,2V,4V, and √2V, we can follow these steps:
Step 1: Square the velocities
First, we need to square each of the velocities:
- V2=V2
- (2V)2=4V2
- (4V)2=16V2
- (√2V)2=2V2
Step 2: Sum the squared velocities
Now, we sum these squared values:
V2+4V2+16V2+2V2=(1+4+16+2)V2=23V2
Step 3: Divide by the number of molecules
Next, we divide the sum of the squared velocities by the number of molecules (which is 4):
Mean=23V24
Step 4: Take the square root
Finally, we take the square root of the mean to find the r.m.s. speed:
Vr.m.s.=√23V24=√23V2
Step 5: Approximate the value
To approximate Vr.m.s., we can use the approximate value of √23:
\sqrt{23} \approx 4.8 \quad \text{(since 4.8^2 = 23.04 )}
Thus,
Vr.m.s.≈4.8V2=2.4V
Final Answer
The r.m.s. speed of the molecules is approximately 2.4V.
---
First, we need to square each of the velocities:
- V2=V2
- (2V)2=4V2
- (4V)2=16V2
- (√2V)2=2V2
Now, we sum these squared values:
V2+4V2+16V2+2V2=(1+4+16+2)V2=23V2
Next, we divide the sum of the squared velocities by the number of molecules (which is 4):
Mean=23V24
Finally, we take the square root of the mean to find the r.m.s. speed:
Vr.m.s.=√23V24=√23V2
To approximate Vr.m.s., we can use the approximate value of √23:
\sqrt{23} \approx 4.8 \quad \text{(since 4.8^2 = 23.04 )}
Thus,
Vr.m.s.≈4.8V2=2.4V
The r.m.s. speed of the molecules is approximately 2.4V.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the velocities of three gas molecules are √7, 4 and 5 m/s, then there Vrms ( in m/s) will be
A4B4√3C2−√73D4√3The velocity of light through media 'A' and 'B' are V and 2V, respectively. The value of sin C is ______ [where 'C' is the critical angle].
A12B13C3D2The velocity of sound waves in an ideal gas at temperatures T1KandT2 are respectively v1andv2 . The rms velocity of gas molecules at these two temperatures are w1ande2 , respectively then
Av1v2=w1w2Bv1v2=√γw1w2Cv1v2=√γ3w1w2Dv1v2=√w1w2
V1, V2, V3 and V4 are the volumes of four cubes of side lengths x cm , 2x cm , 3x cm and 4x cm respectively. Some statements regarding these volumes are given below V1+V2+2V3<V4 (2) V1+4V2+V3<V4 (3) 2(V1+V3)+V2=V4 Which of these statements are correct? (a) 1 and 2 (b) 2 and 3 (c) 1 and 3 (d) 1, 2 and 3
View SolutionA proton a deutron and an α particle are accelerated through potentials of V,2V and 4V respectively. Their velocity will bear a ratio
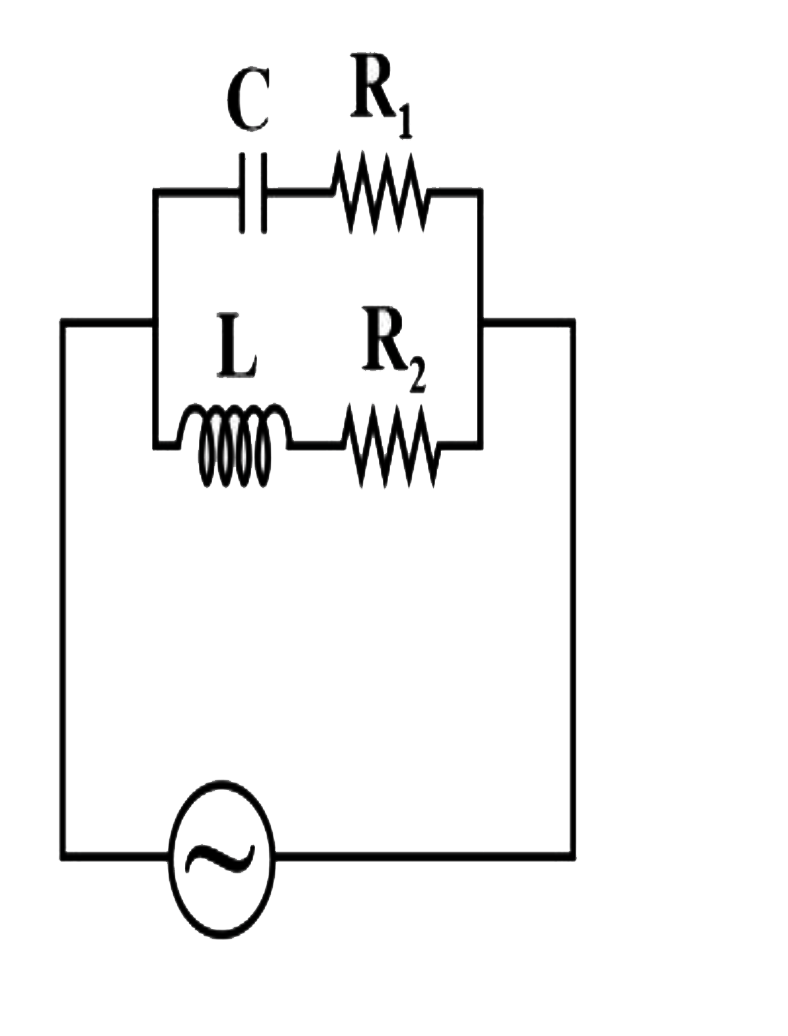
View SolutionIn the given circuit the R.M.S values of voltages across the capacitor C, inductor L and resistor R1 are 12V, 10V and 5 V respectively. Then the peak voltage across R2 is
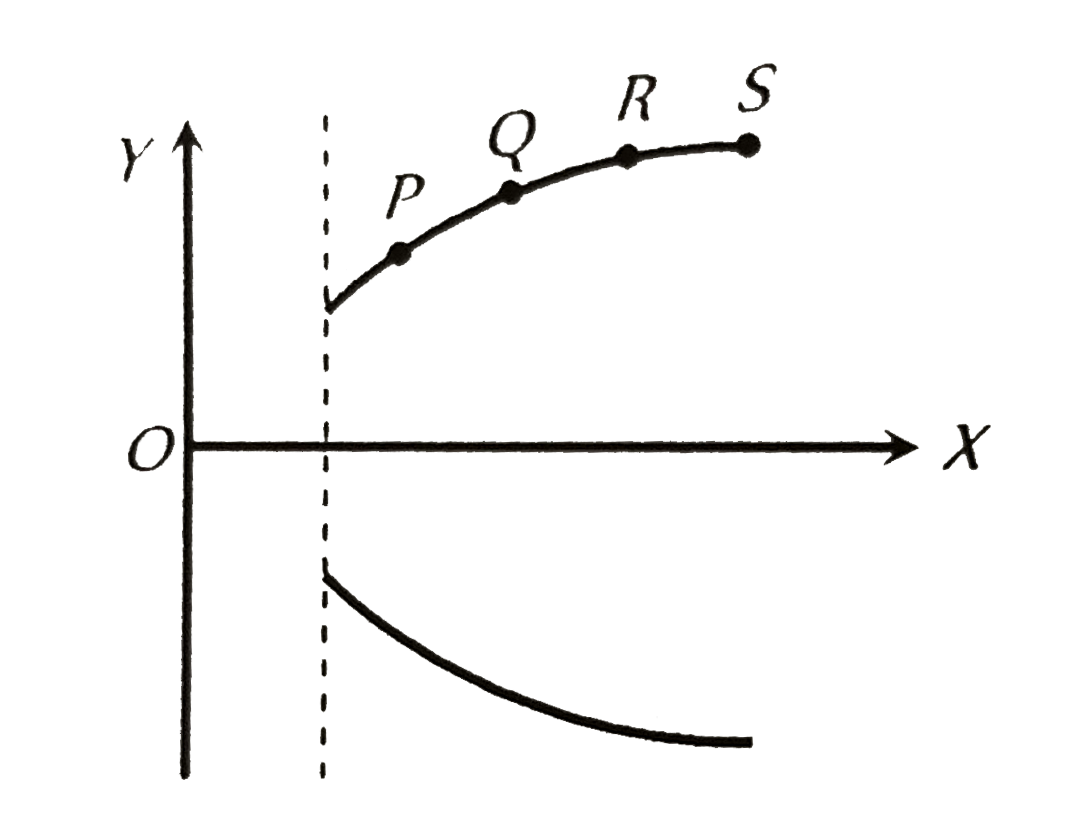
View SolutionIn a parabola spectrograph, the velocities of four positive ions P,Q,R and S are v1,v2,v3 and v4 respectively
View SolutionVV,VR,VG are the velocities of violet, red and green light , respectively, in a glass prism. Which among the following is a correct relation?
View Solution