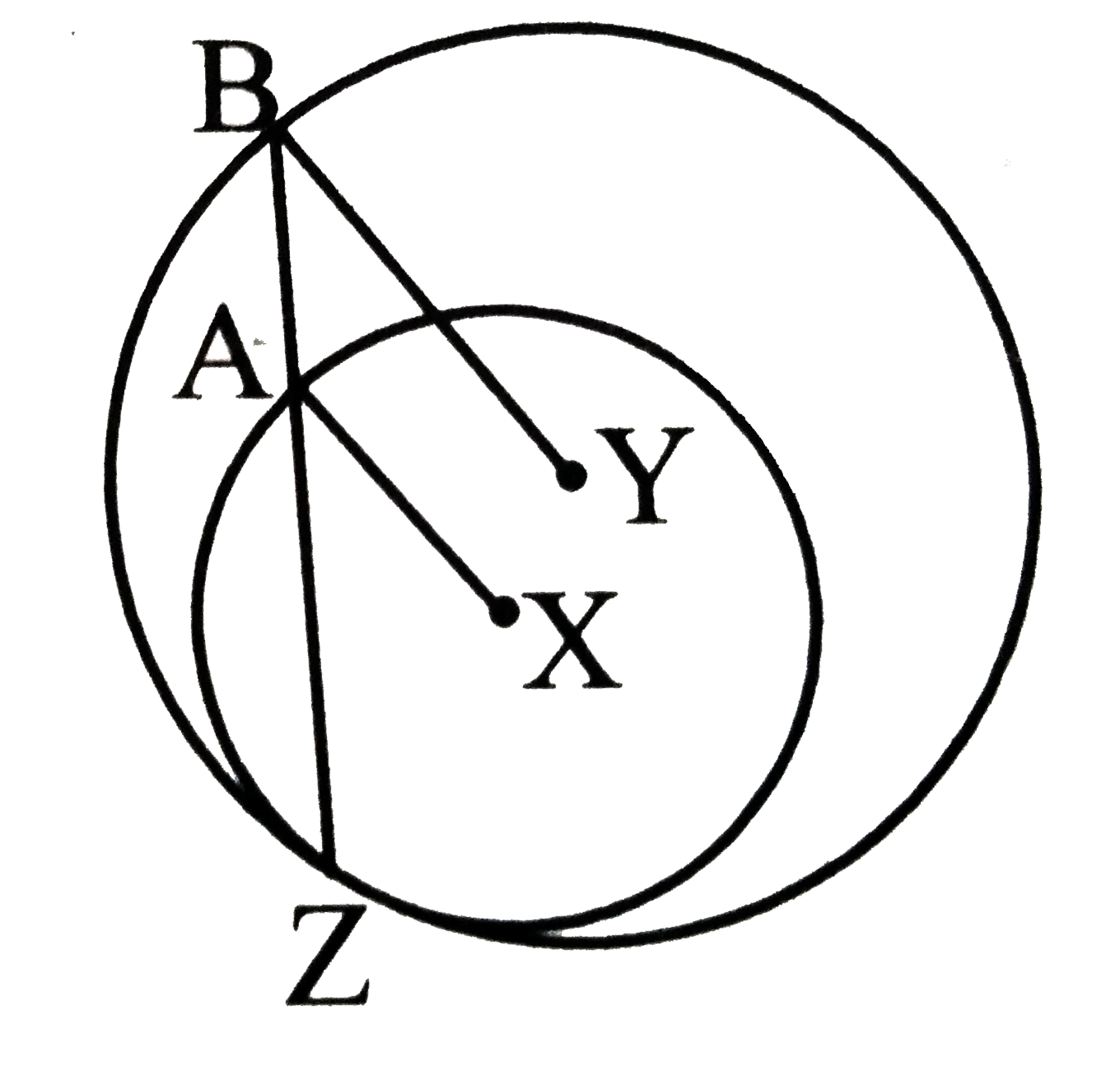
In the adjoining figure, circles with centres X and Y touch internally
at point Z. Seg BZ is a chord of bigger circle and it intersects smallest
circle at point A. prove that, seg AX ∣∣seg BY.
 Solution in Marathi
Solution in Marathi
The correct Answer is:∴ seg AX ∣∣ seg BY
Step by step video & image solution for In the adjoining figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smallest circle at point A. prove that, seg AX ||seg BY. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Activities for Practice
3 Videos
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Multiple Choice Question
27 Videos
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set 3.5
3 Videos
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - CHAPTER-1 :Linear Equations in Two Variable
1 Videos
- CO-ORDINATE GEOMETRYBOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT
15 Videos
Similar Questions
Complete the activity by filling the boxes.
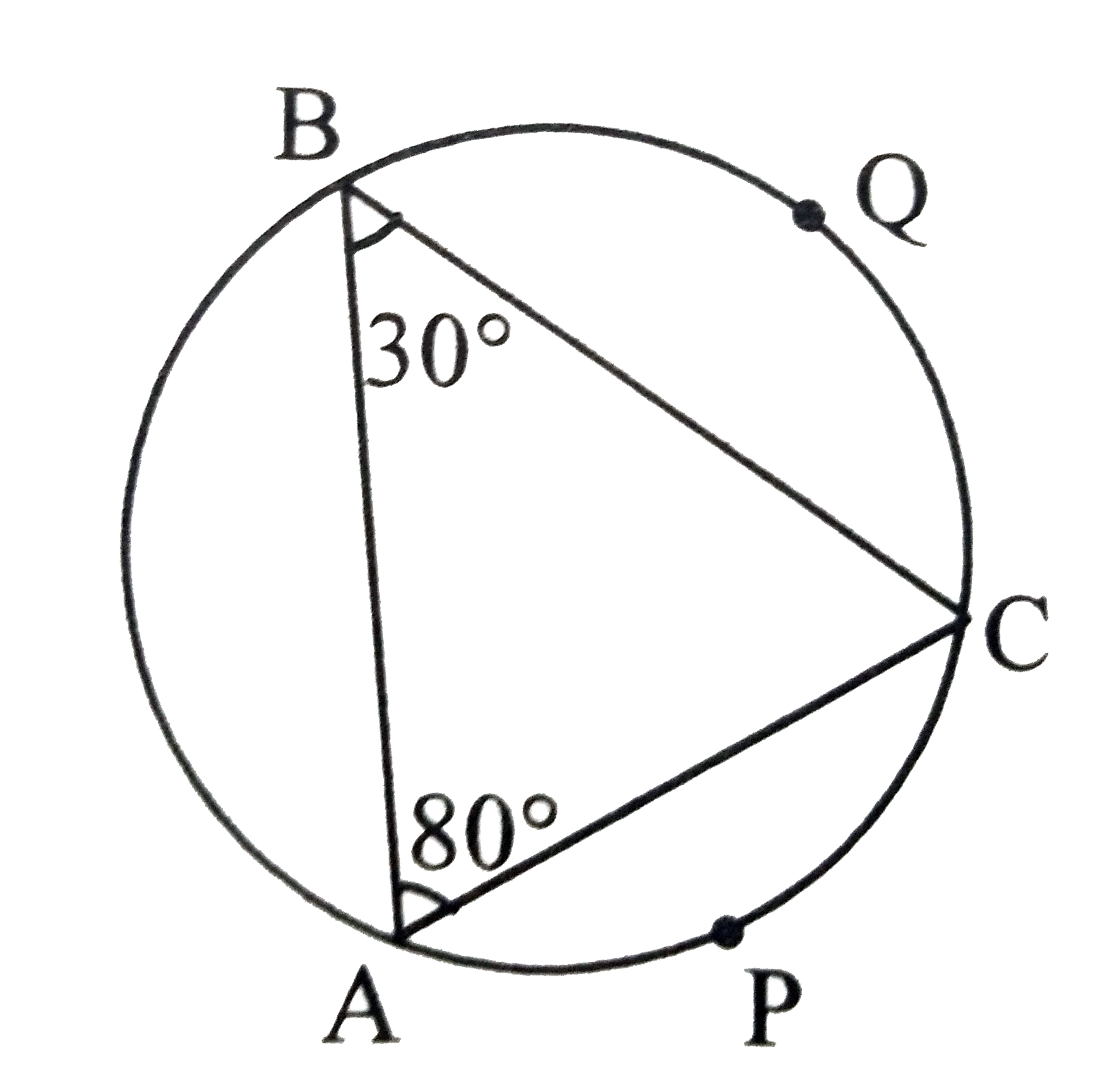
In the given figure , ∠BAC=80∘ ,∠ABC=30∘ and
m(arcBQC)=160∘.
Find (i) m(arcAPC) (ii) m(arcAB).
View SolutionConcentric Circles have the same______.
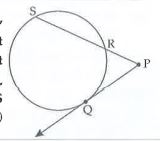
View SolutionIn the adjoining figure, point Q is the point of contact of tangent and the circle. If PQ=12, PR=8, then find PS and RS.
View SolutionSum of two numbers is 97. If the greater number is divided by the the smaller, the quotient is 7 and the remainder is 1. Find the numbers.
View SolutionChoose the correct alternative.
(i) The distance of Q (3,-1) from the origin is
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

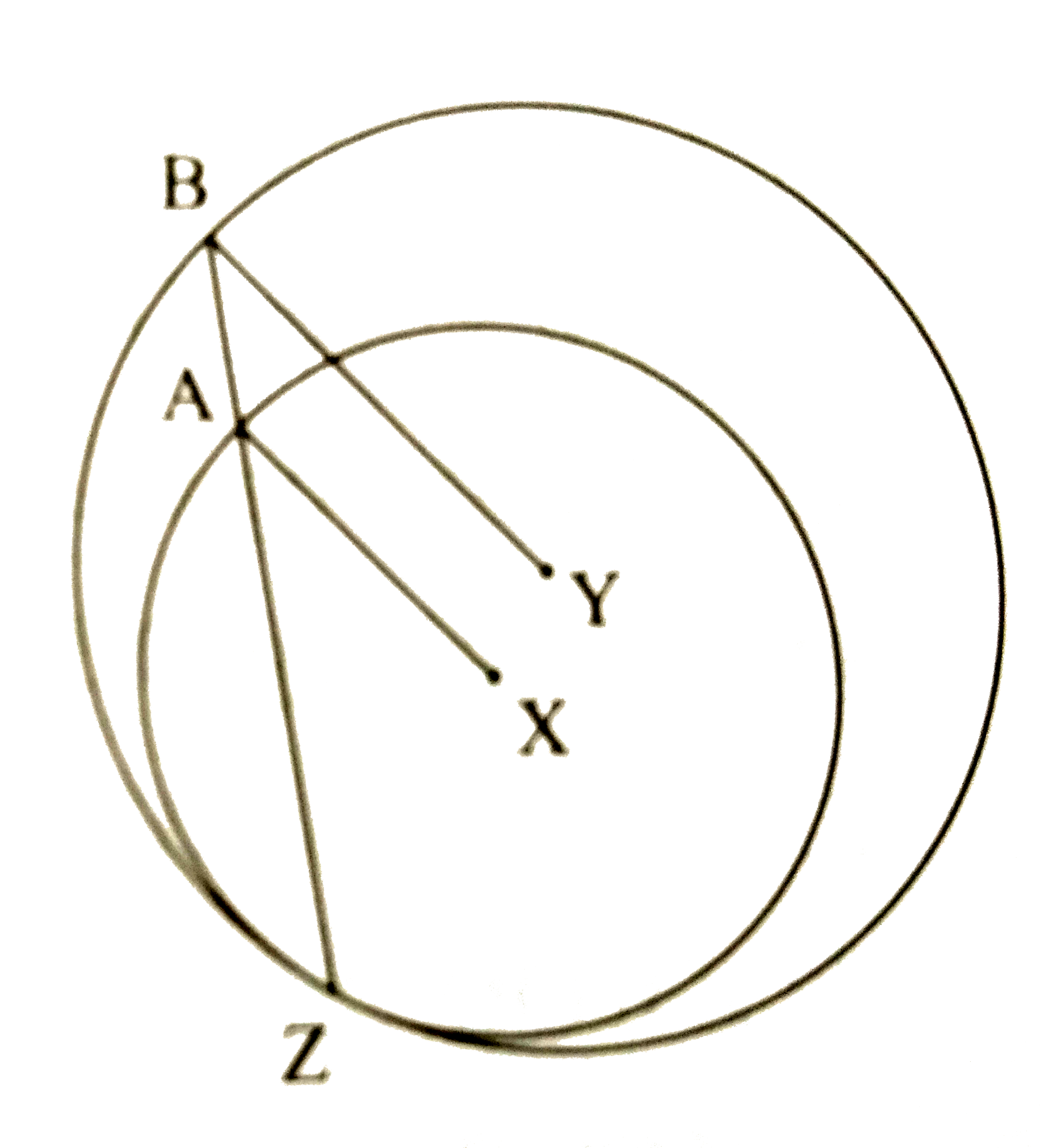
View SolutionIn the figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smaller circlea t point A. Prove that , seg AX ∣∣ seg BY
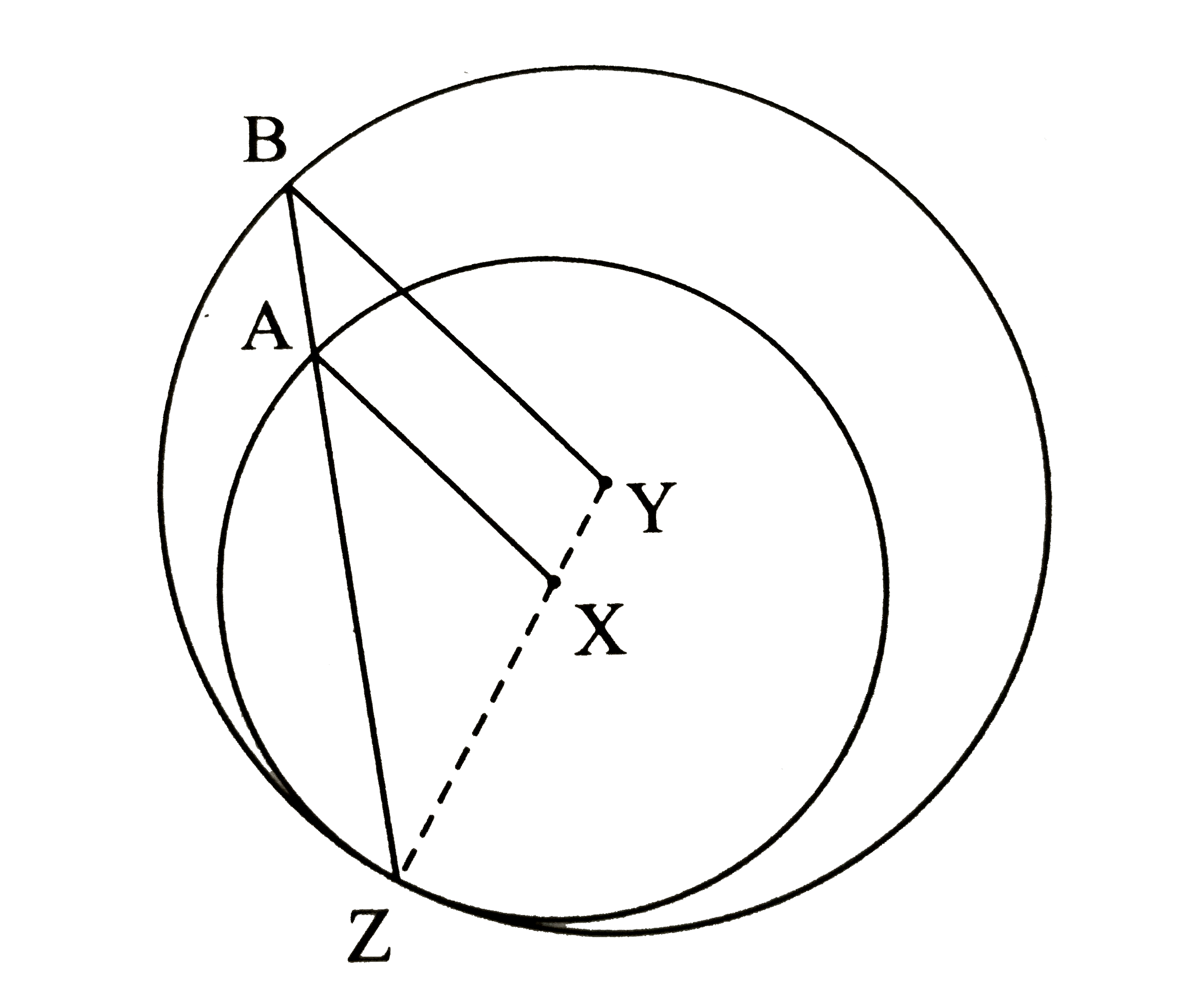
View SolutionIn the figure , circles with centres X and Y touch internally at point Z. Seg BZ is the chord of bigger circle and it intersects smaller k circle at point A.
Prove that seg AX∣∣ seg BY.
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.

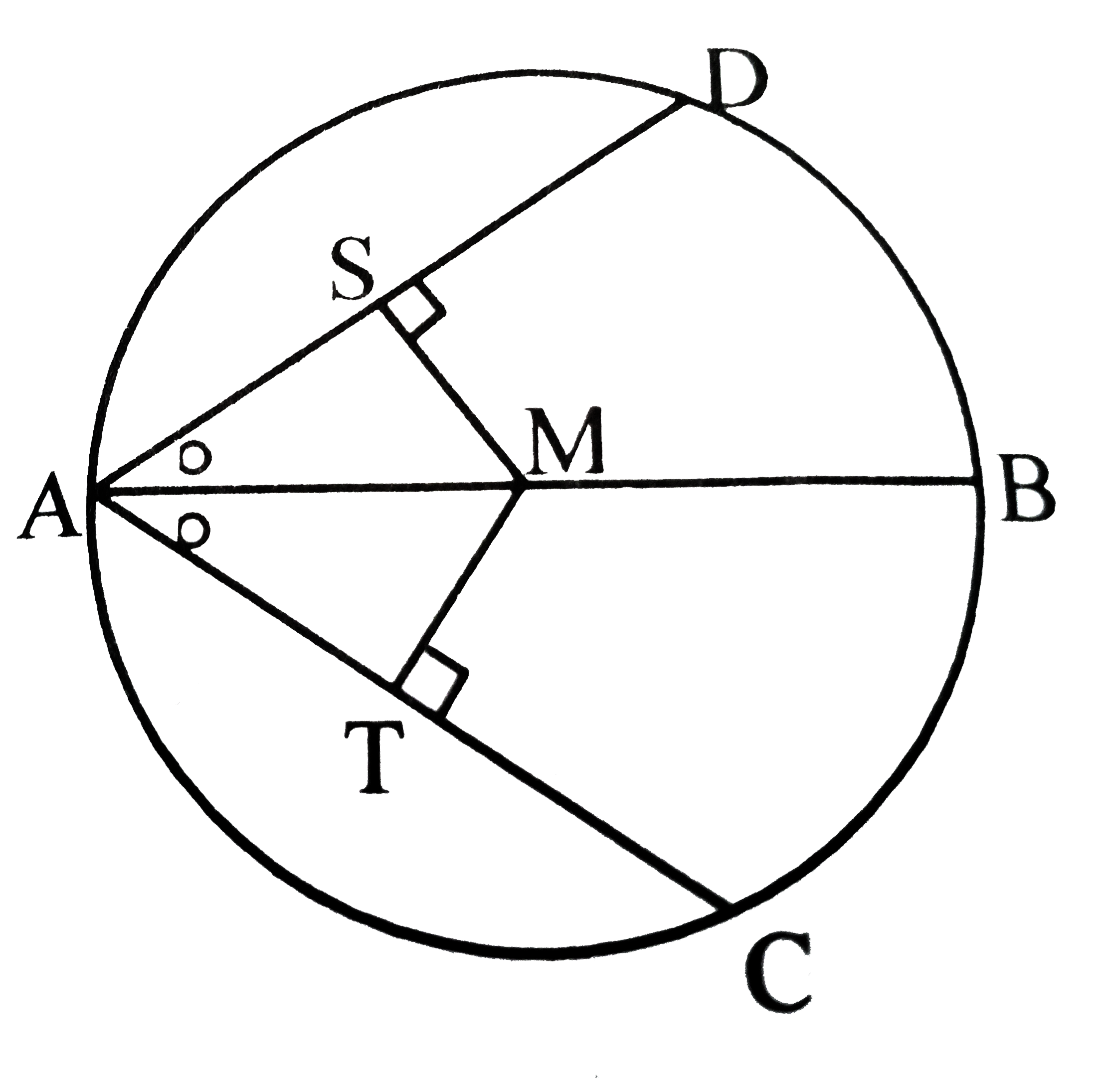
View SolutionIn the adjoining figure, M is the centre of the circle and seg AB is a diameter. Seg MS⊥ chord AD, seg MT ⊥ chord AC, ∠DAB≅∠CAB.
Prove that : chord AD≅ chord AC.
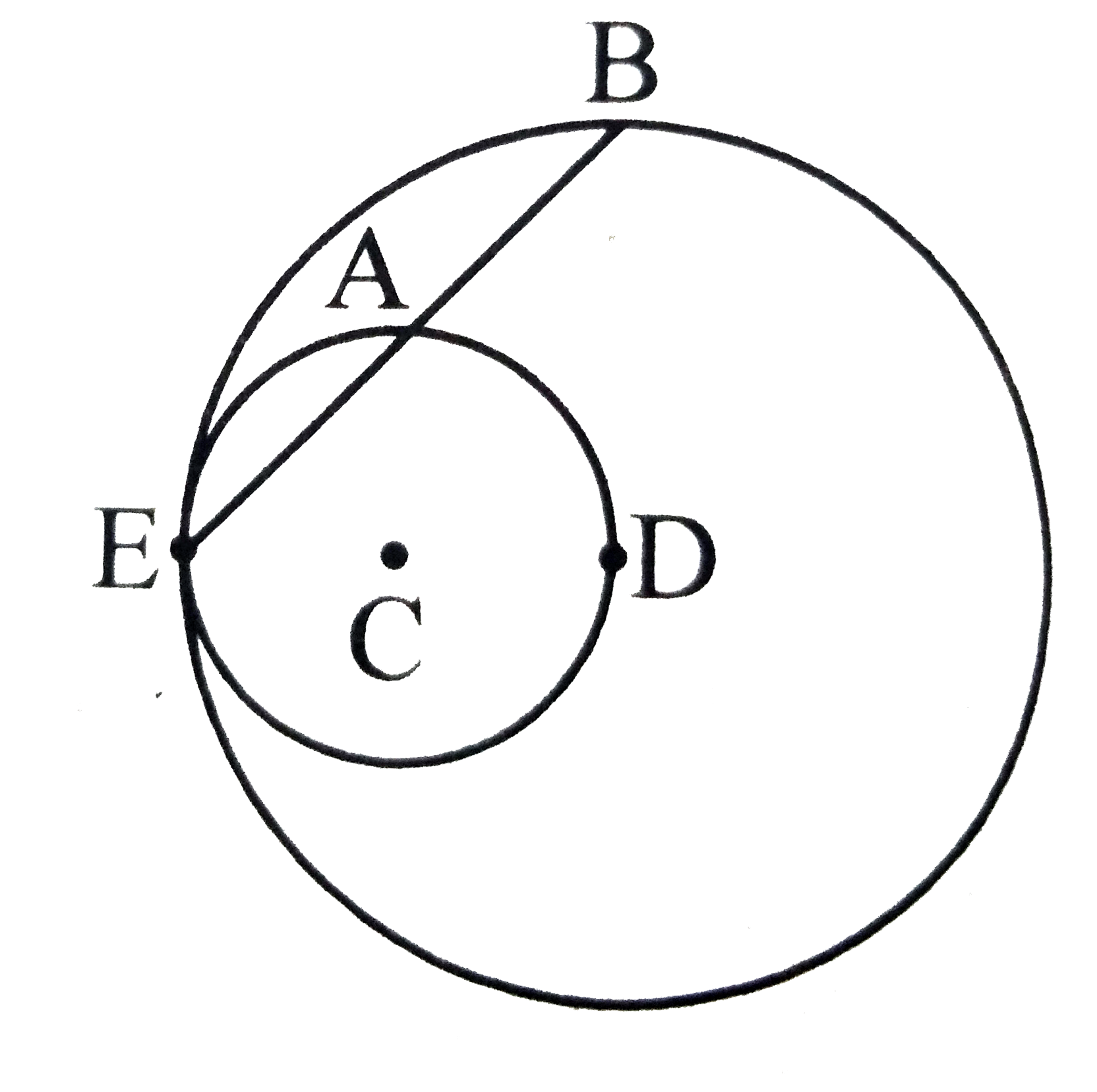
View SolutionIn the adjoining figure , circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the other circle intersects innet circle at point A. Prove that, seg EA≅seg AB.
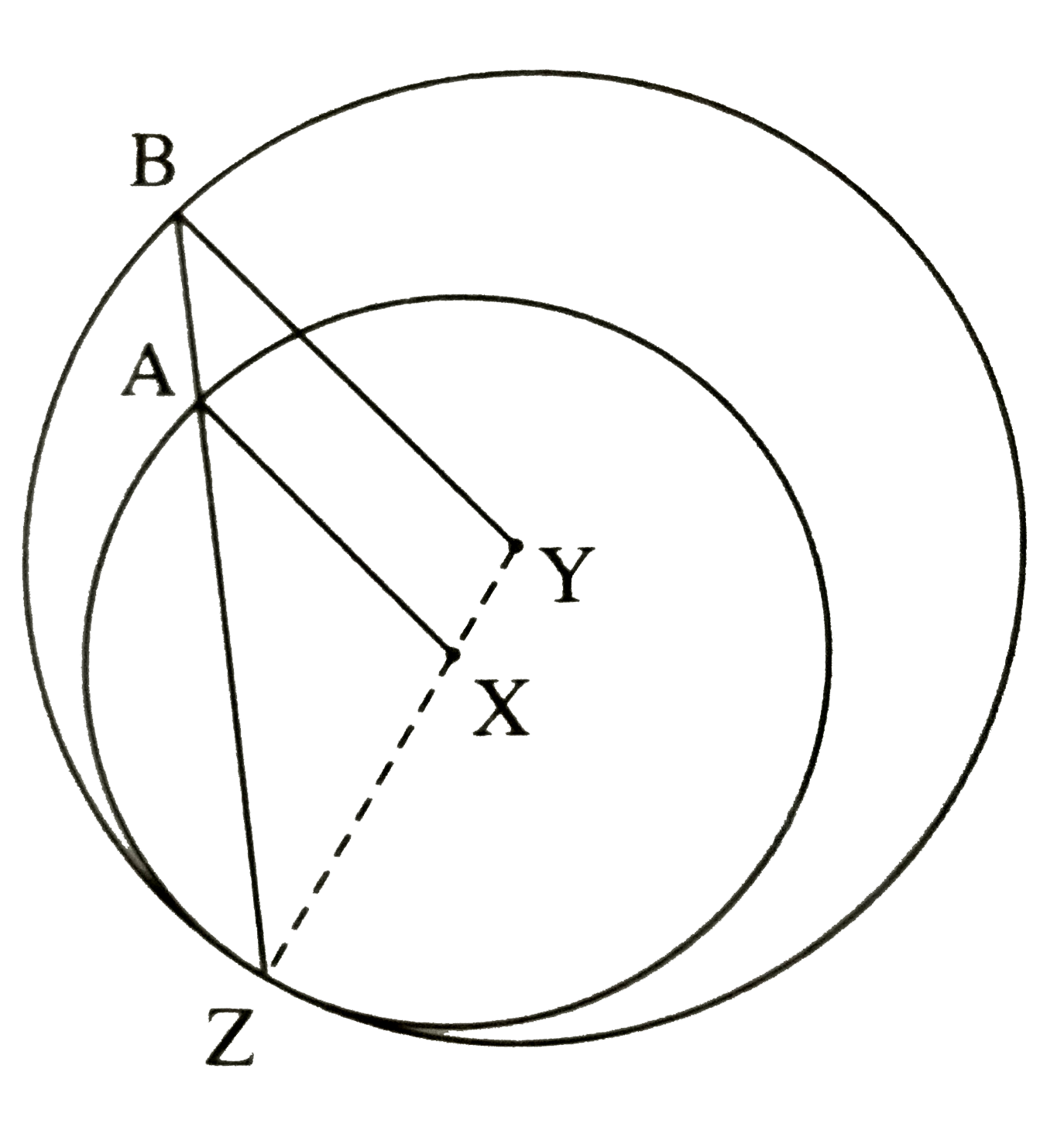
View SolutionIn the figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smaller circle at point A. Prove that, seg AX || seg BY.
View SolutionIn figure, circles with centers C and D touch internally at point E. D lies on the inner circle. Chrd EB of the outer circle intersects inner circle at point A. Prove that, seg EA ≅ seg AB.

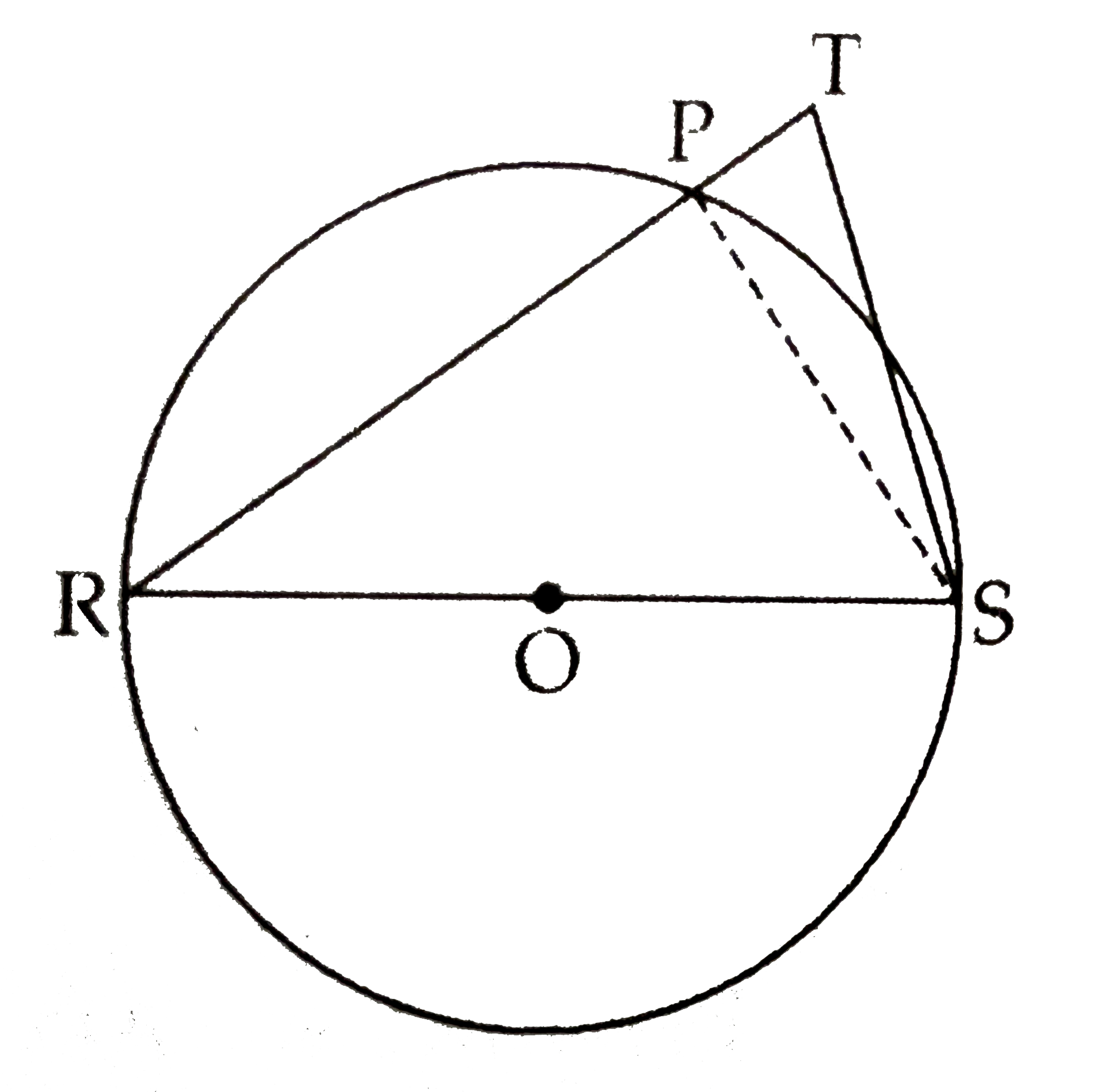
View SolutionIn the adjoining figure seg RS is the dianeter of the circle with centre 'O' . Point T is in the exterior of the circle . Prove that ∠RTS is an acute angle.
View Solution
