In the figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smaller circle at point A. Prove that, seg AX || seg BY.
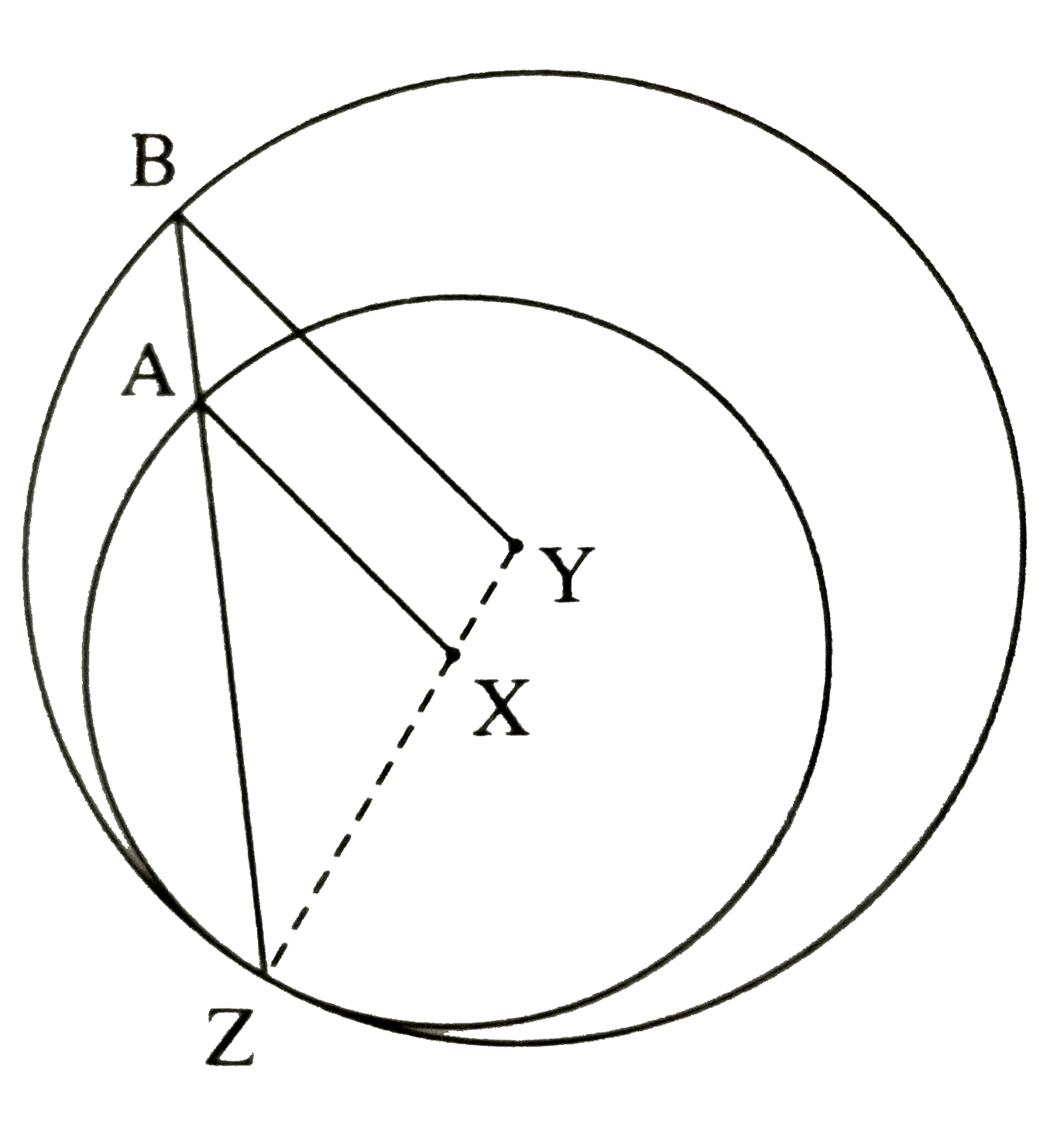
Step by step video & image solution for In the figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smaller circle at point A. Prove that, seg AX || seg BY. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions
10 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.5
6 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
In the figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smaller circlea t point A. Prove that , seg AX ∣∣ seg BY
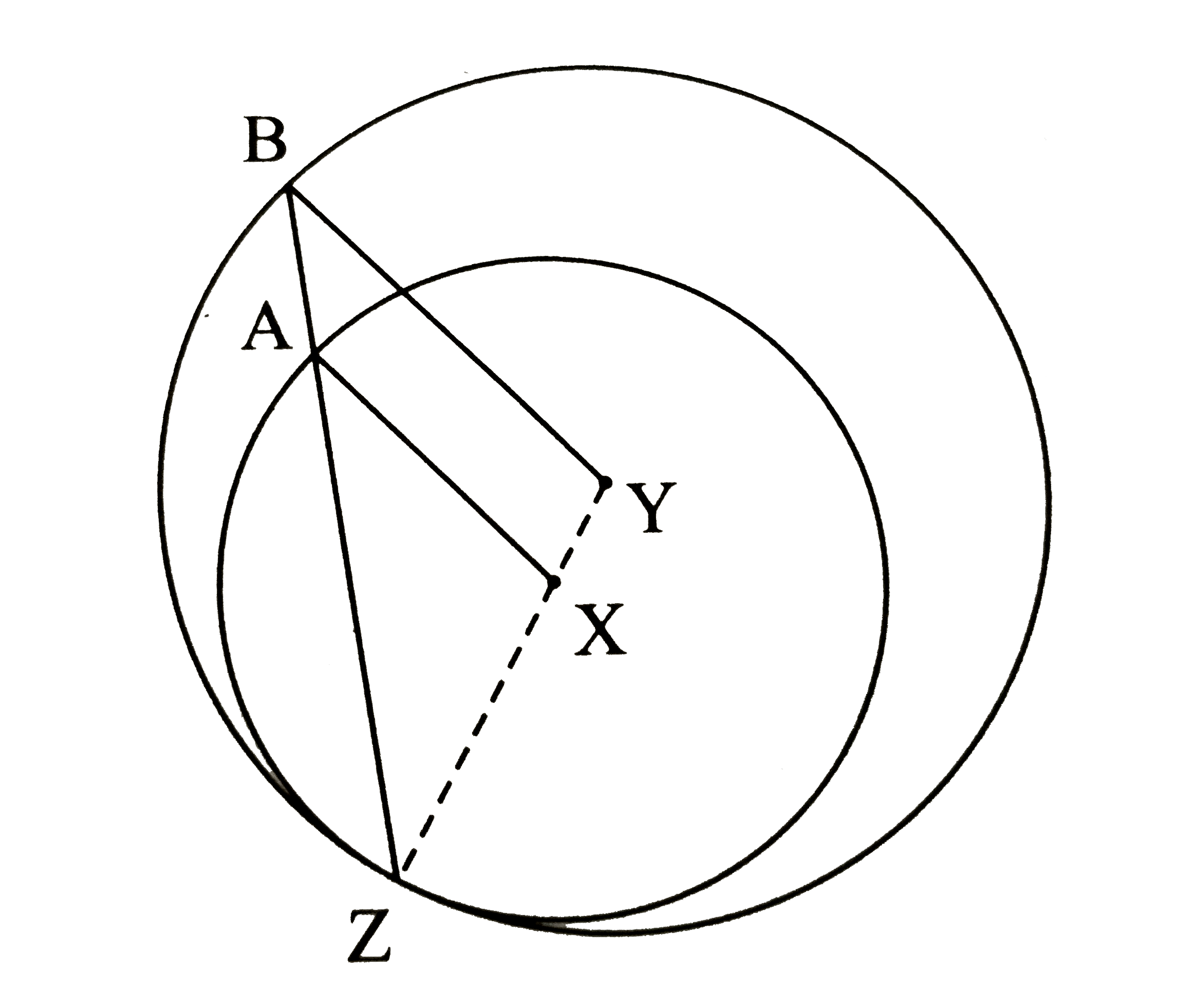
View SolutionIn the figure , circles with centres X and Y touch internally at point Z. Seg BZ is the chord of bigger circle and it intersects smaller k circle at point A.
Prove that seg AX∣∣ seg BY.
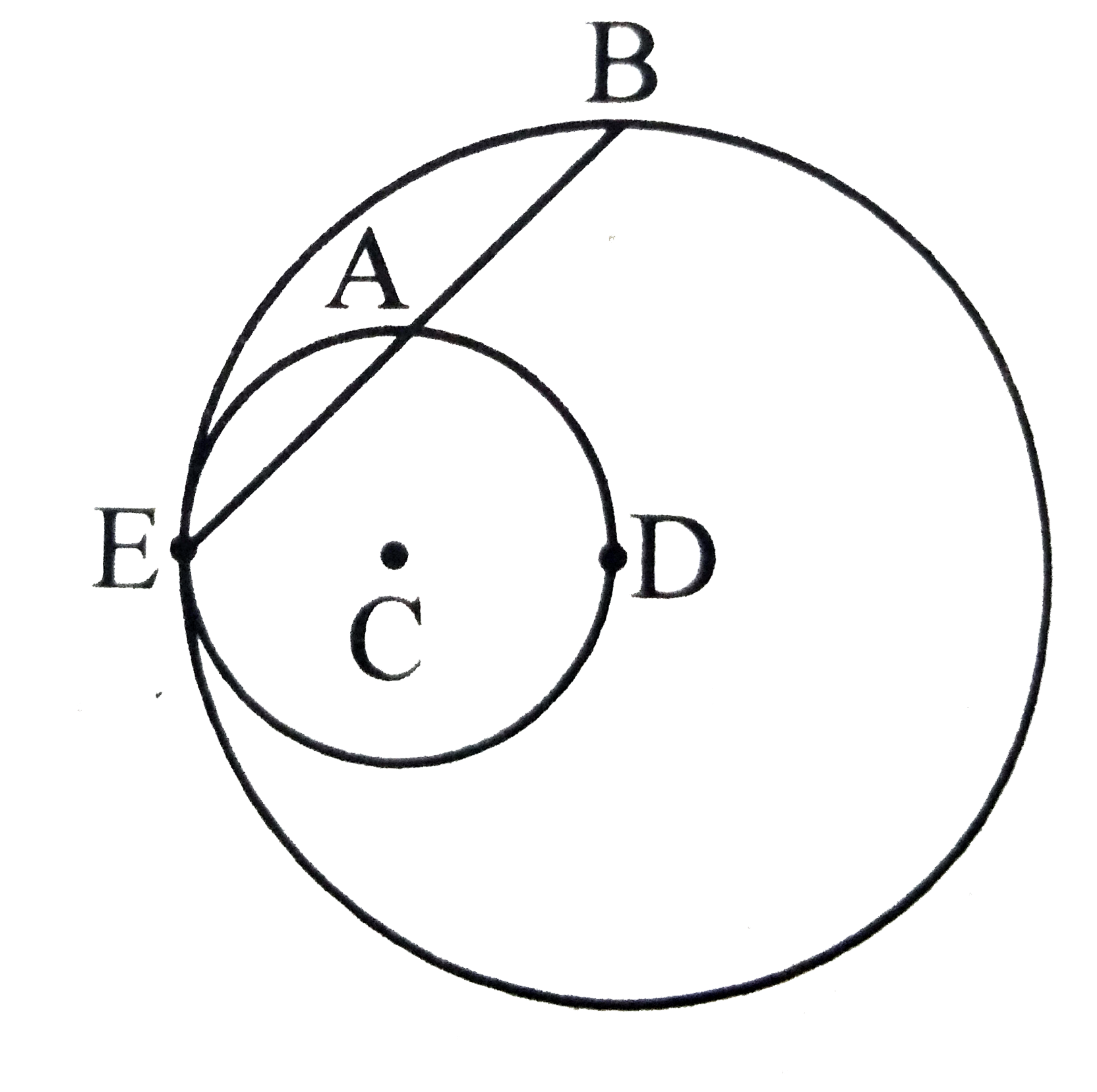
View SolutionIn figure, circles with centers C and D touch internally at point E. D lies on the inner circle. Chrd EB of the outer circle intersects inner circle at point A. Prove that, seg EA ≅ seg AB.
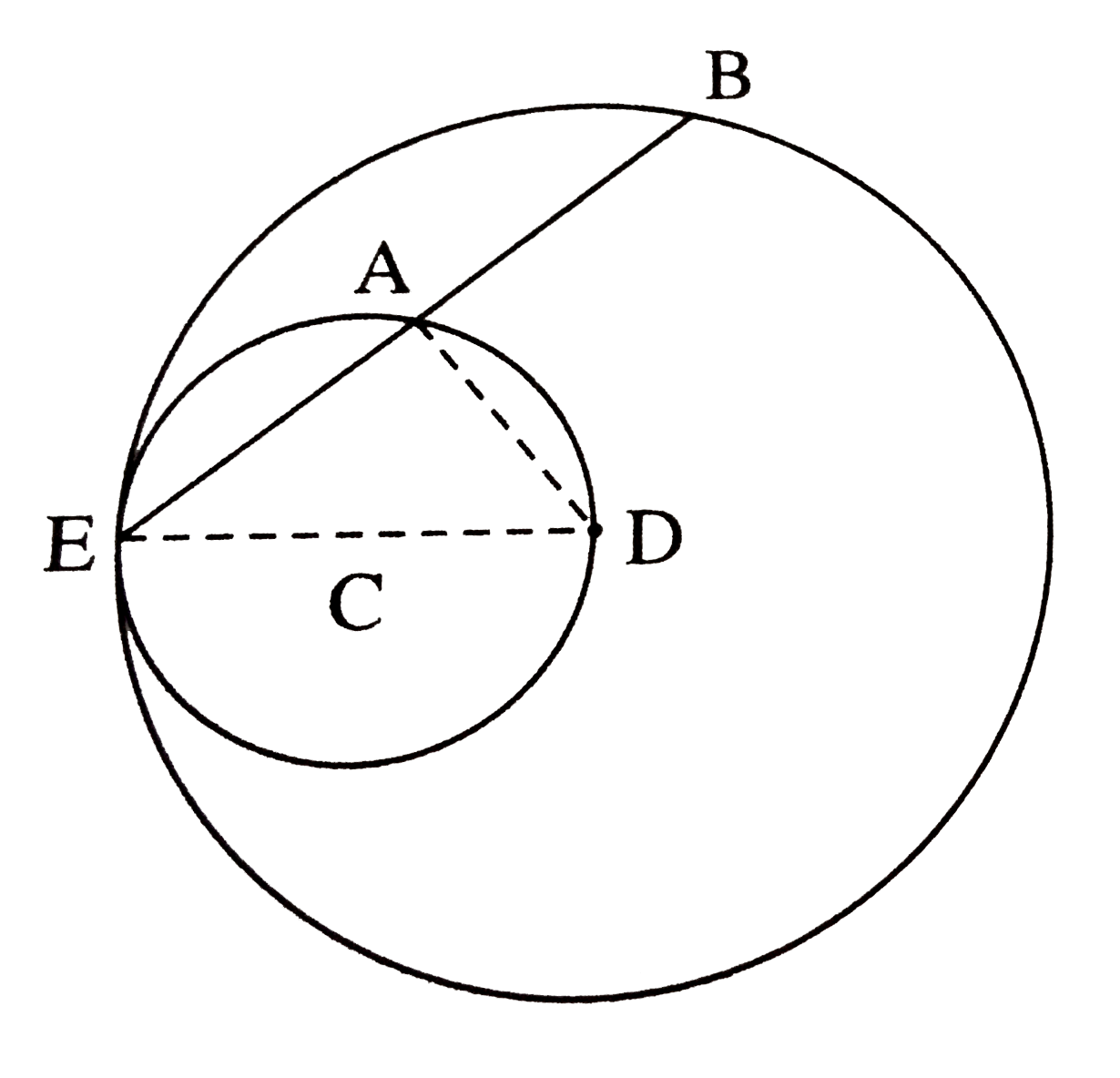
View SolutionIn the adjoining figure , circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the other circle intersects innet circle at point A. Prove that, seg EA≅seg AB.
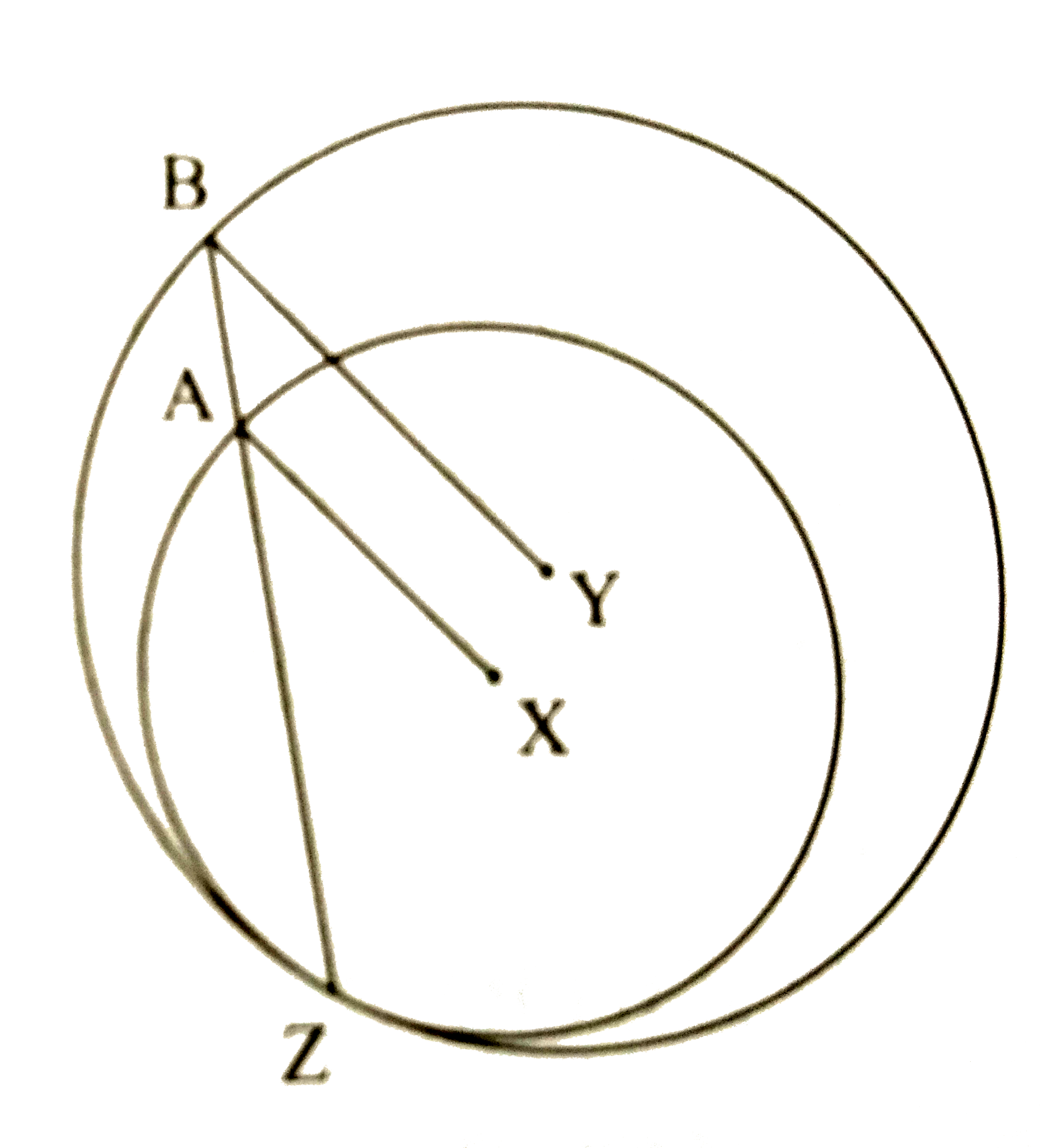
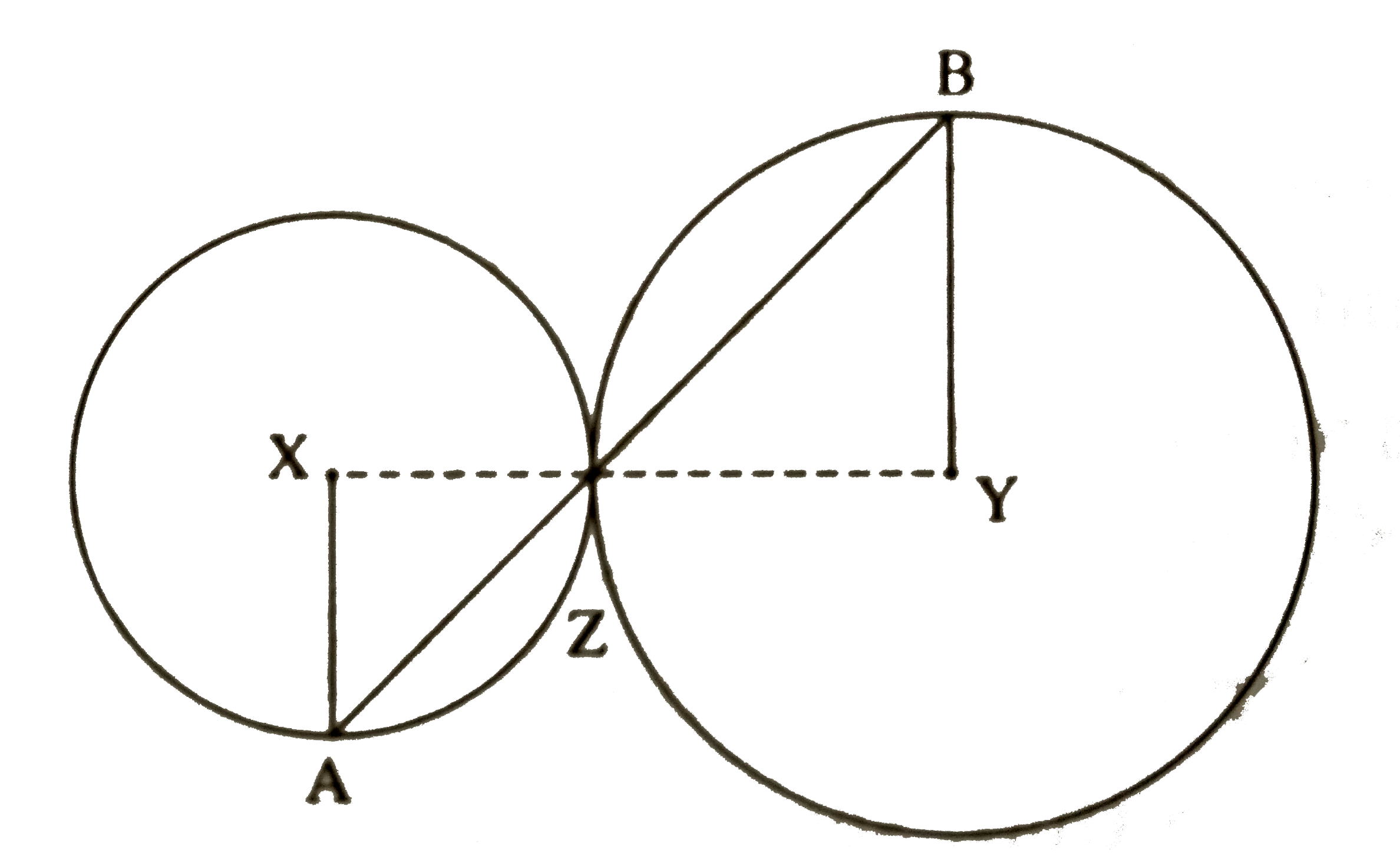
View SolutionIn the figure, circles with centres X and Y touch each other at point Z. A secant passing through Z intersects the circles at points A and B respectively. Prove that, raduis XA || radius YB. Fill in the blanks and complete the proof:
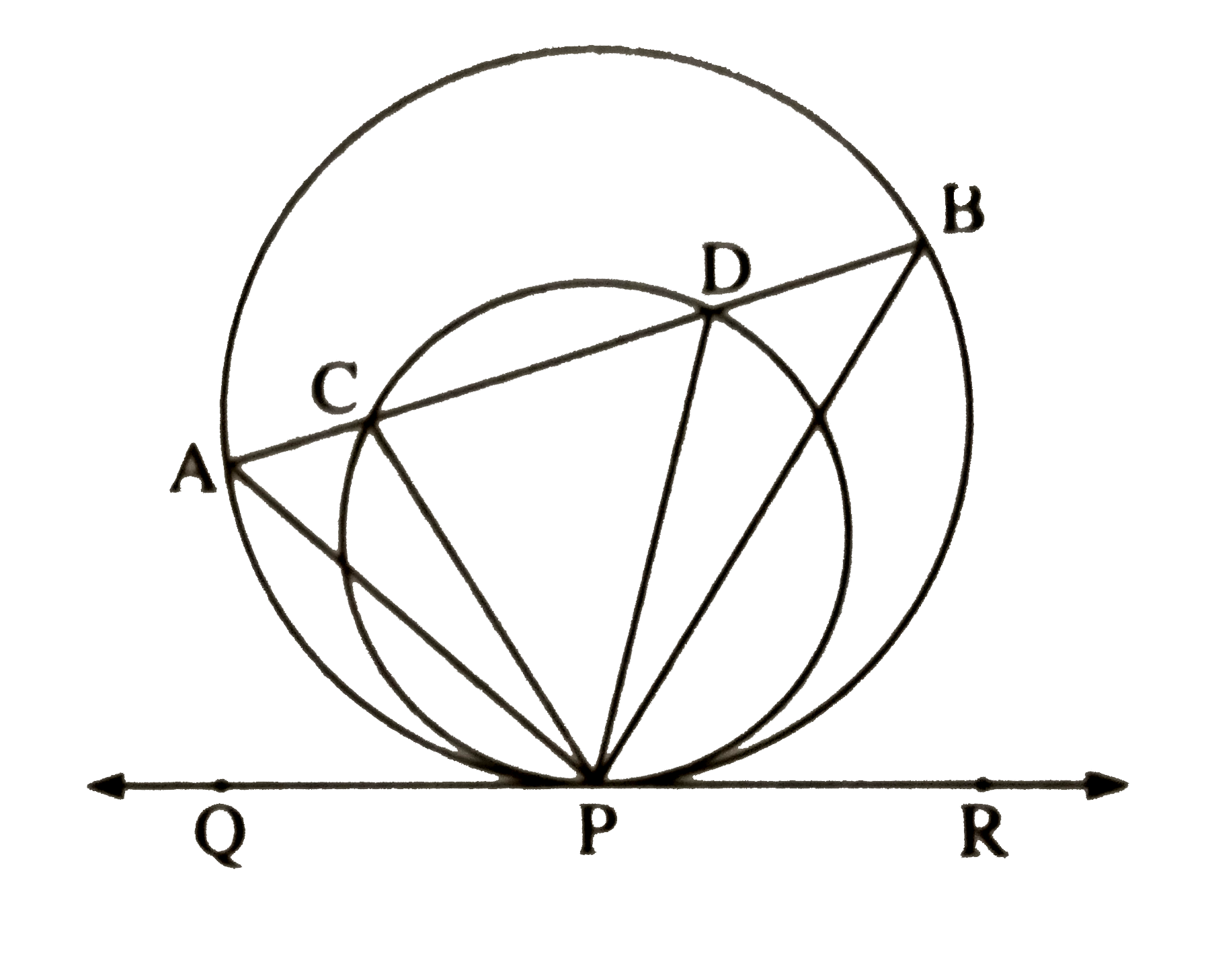
View SolutionIn the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove ∠CPA≅∠DPB.
View SolutionIn Figure, circle C(O,r)andC(O′r2) touch internally at a point. AandAB is a chord of the circle C(O,r) intersecting C(O′,r2) at C . Prove that AC=CB
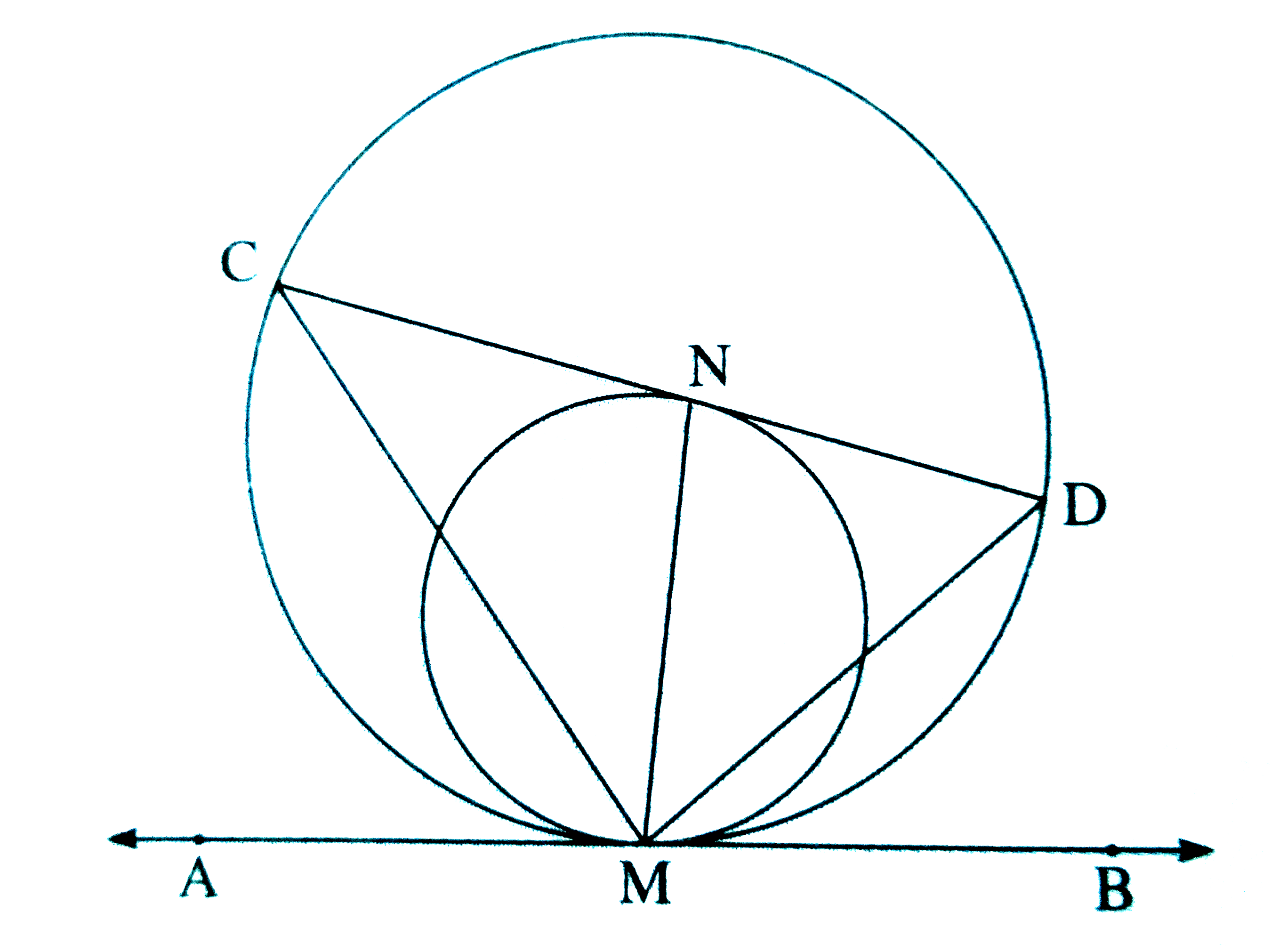
View SolutionIn the figure, M is the point of contact of two internally touching circles. The chord CD of the bigger circle touches the smaller circle at point N. Line AMB is their common tangent. Prove MN bisects ∠CMD
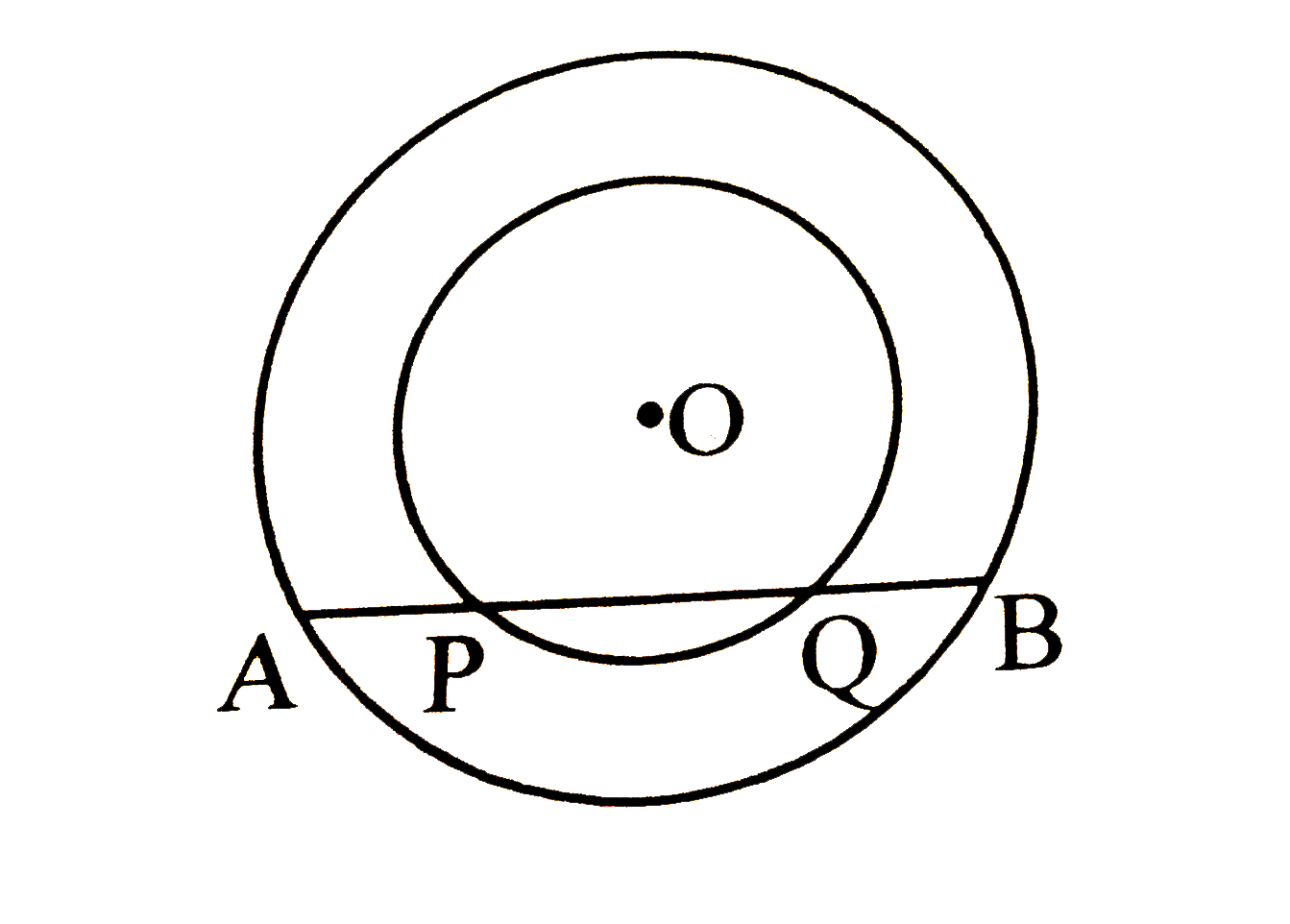
View SolutionIn the given figure, centre of two circles is O. Chord AB of bigger circle intersects the smaller circle in points P and Q . Show that AP = BQ.
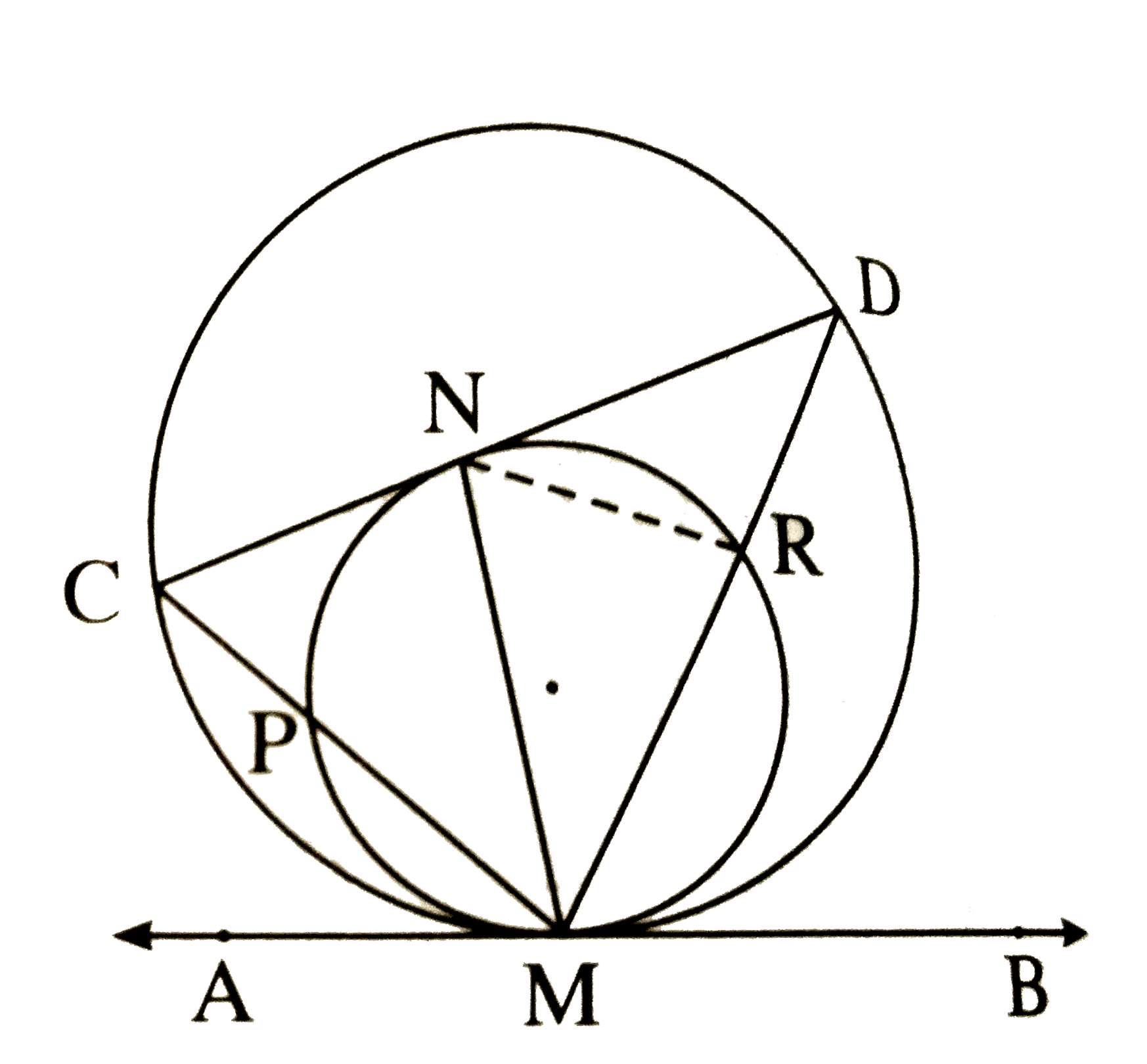
View SolutionLet M be a point of contact of two internally touching circles. Let line AMB be their common tangent. The chord CD of the bigger circle touches the smaller circle at the point N. Chord CM and chord DM of the bigger circler intersect the smaller circle at the points P and R respectively.
Prove that ∠CMN≅∠DMN.
Construction : Draw seg NR.
View Solution
