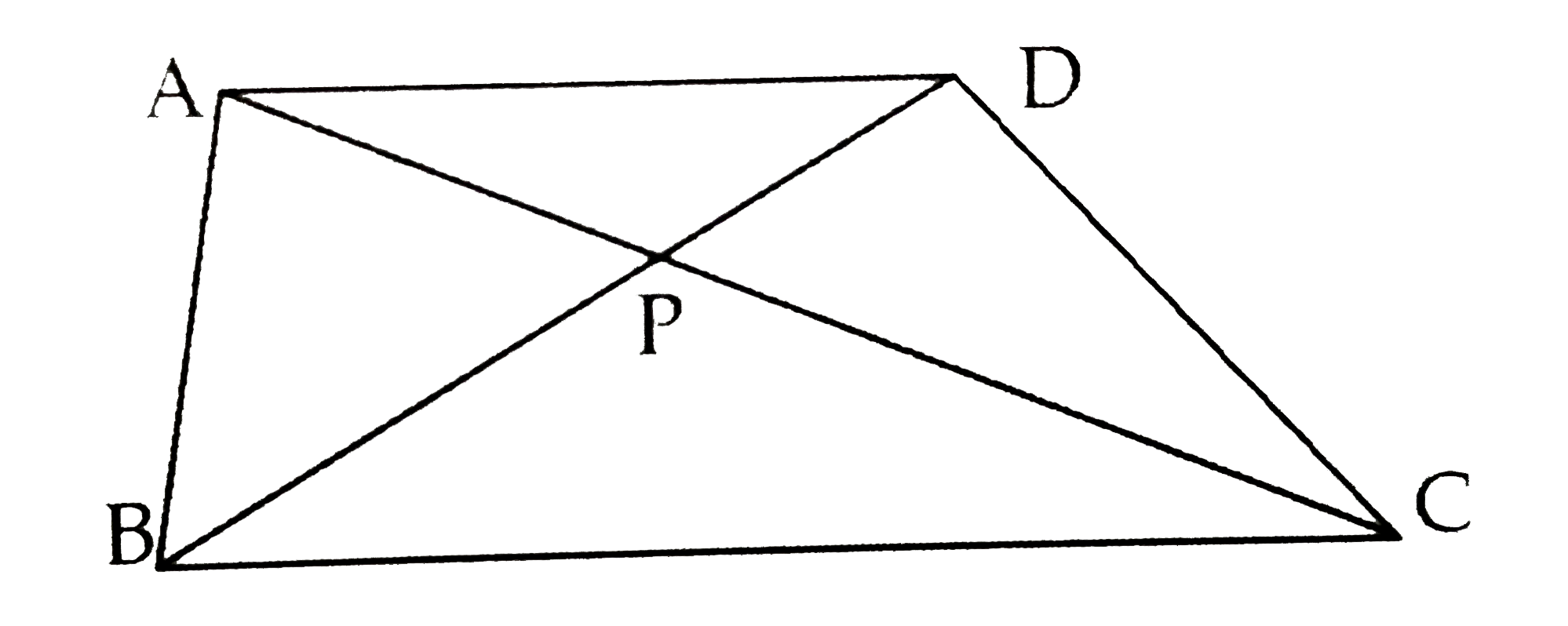
In □ABCD , side BC∣∣ side AD. Digonals AC and BD
intersect each other at P. If AP=13AC then prove DP=12BP.Solution in Marathi
The correct Answer is:∴DQ=12BQ
Step by step video & image solution for In squareABCD , side BC|| side AD. Digonals AC and BD intersect each other at P. If AP=(1)/(3)AC then prove DP=(1)/(2)BP. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Pythagoras theorem
2 Videos
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Circle
7 Videos
- BOARD QUESTION PAPER: MARCH 2019BOOK - TARGET PUBLICATIONCHAPTER - BOARD QUESTION PAPER: MARCH 2019EXERCISE - (Solve the following questions (Any three):
2 Videos
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Chapter Assessment
14 Videos
Similar Questions
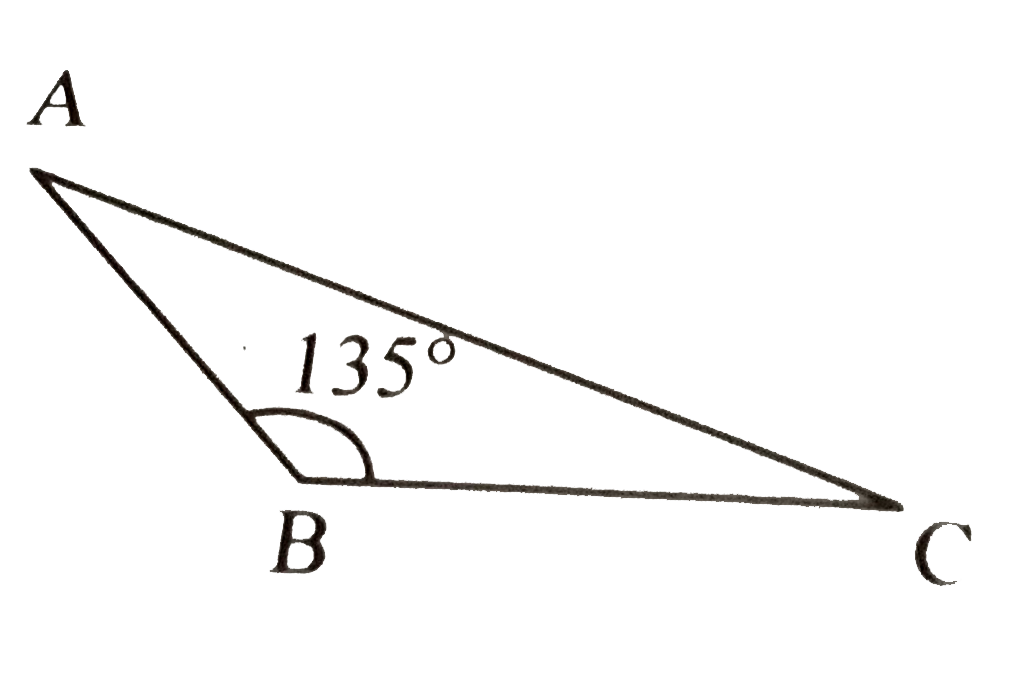
In ΔABC,∠ABC=135∘ . Prove that : AC2=AB2+BC2+4A(ΔABC) .
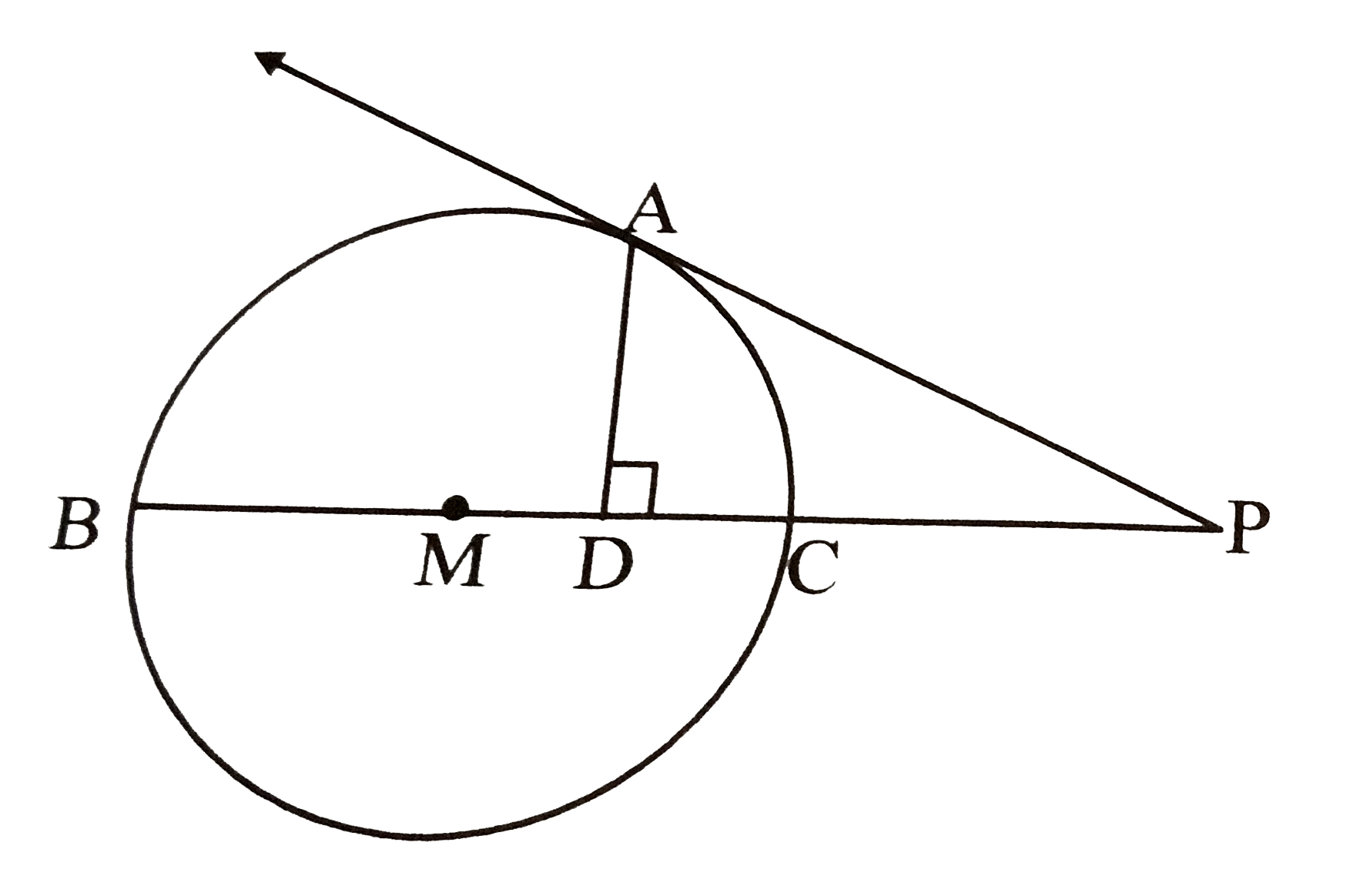
View SolutionIn the adjoining figure, BC is a diameter of the circle with centre M.
PA is a tangent at A from P, which is a point on line BC. AD ⊥ BC
prove that DP2=BP×CP−BD×CD
View SolutionIn ΔPQR ,seg PM is a median , PM=9 and PQ∘+PR2=290. Find the length of QR.
View SolutionIf two circles with diameter 8cm and 6 cm touch externally,
then the distance between their centres is ______.
View SolutionIn ABCD side BC | side AD.Seg AC and seg BD intersect in point Q.If AQ=1/3 AC then show that DQ=(1)/(2)BQ
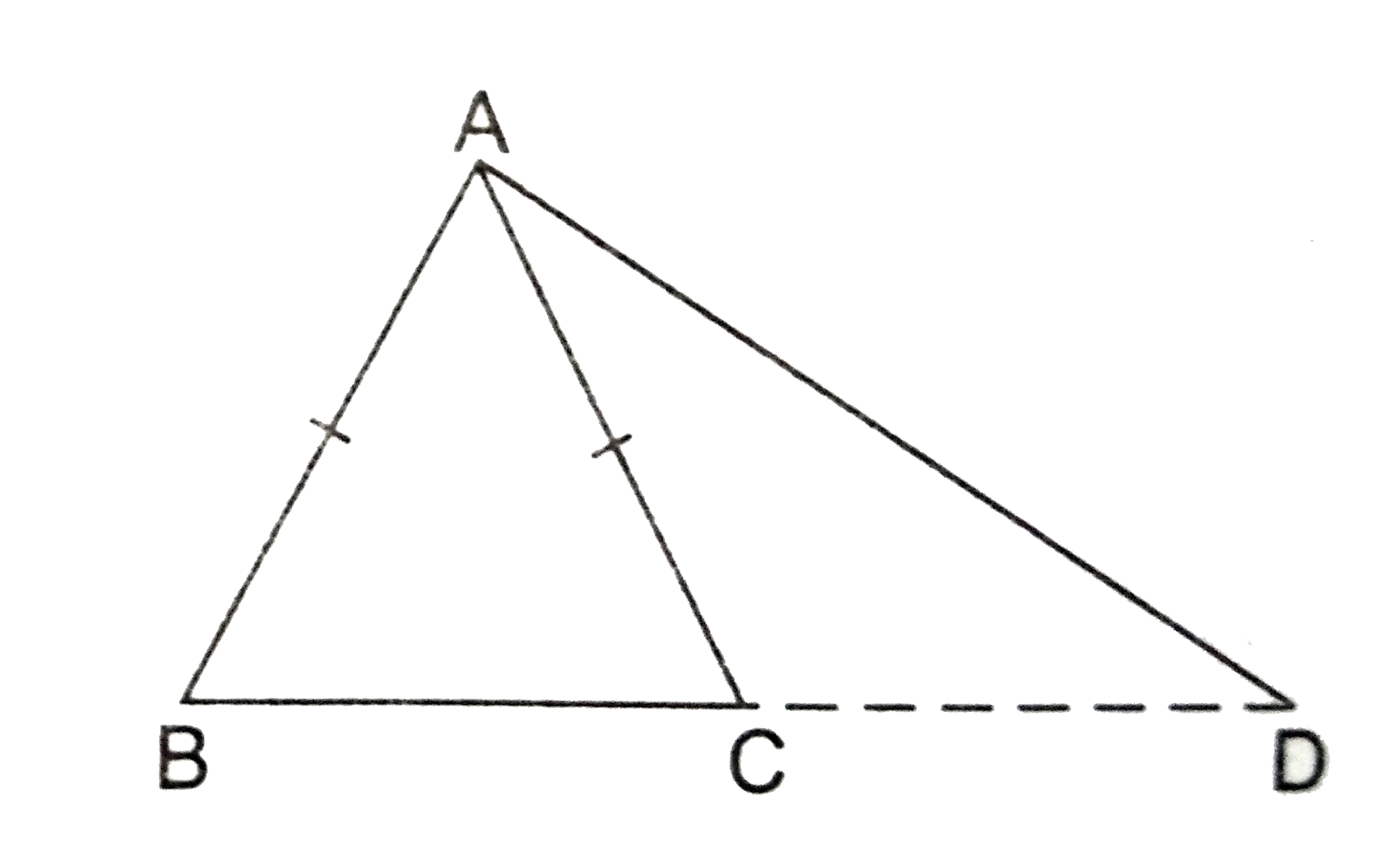
View SolutionIn ΔABC,AB=AC. Side BC is produced to D. Prove that (AD2−AC2)=BD⋅CD.
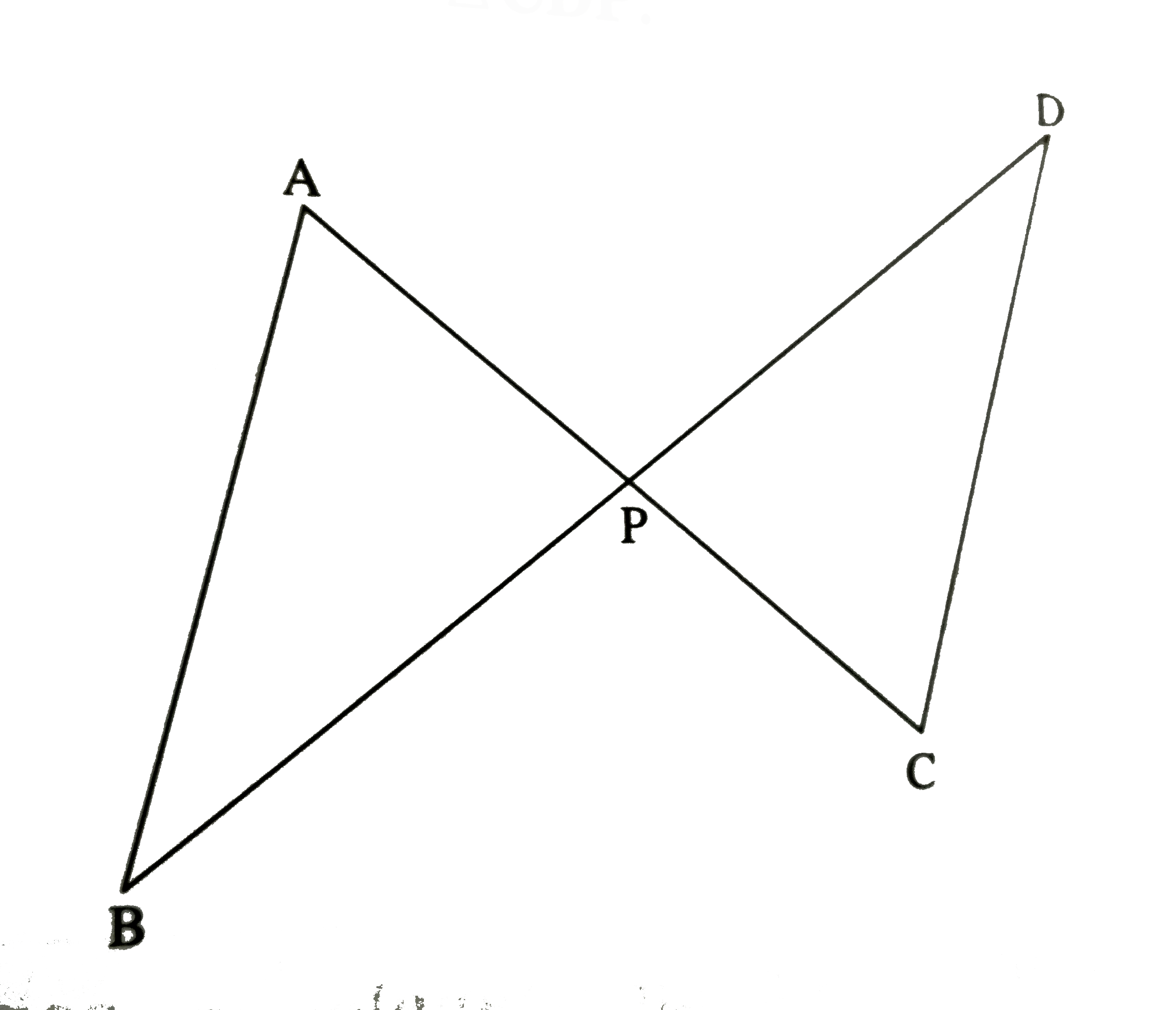
View SolutionIn the figure, seg AC and seg BD intersect each other in point P and APCP=BPDP. Prove that ΔABP~ΔCDP.
View SolutionIn □ABCD , side BC∣∣ side AD. Digonals AC and BD intersect each other at P. If AP=13AC then prove DP=12BP.
View SolutionIn the figure, set aC and seg BD intersect each other in point P and APCP=BPDP. Prove that ΔABP~ΔCDP.
View SolutionIn □ABCD, seg AD∣∣ seg BC. Diagonal AC and digonal BD intersect each other in point P. Then show that APPD=PCBP.
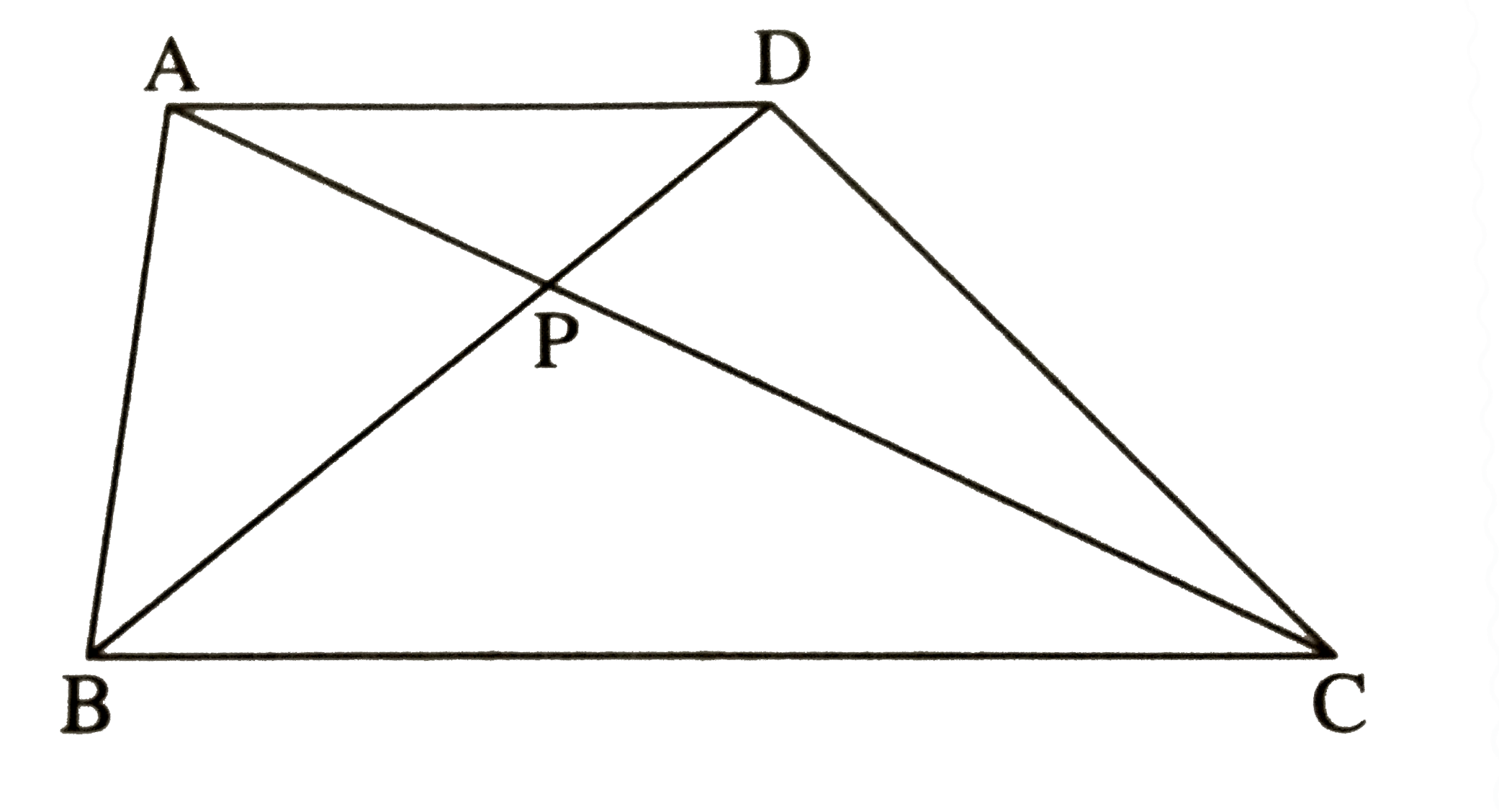
View Solution□ABCD is a parallelogram. P is the midpoint of side CD. Seg BP meets diagonal AC at X. Prove that 3AX=2AC.
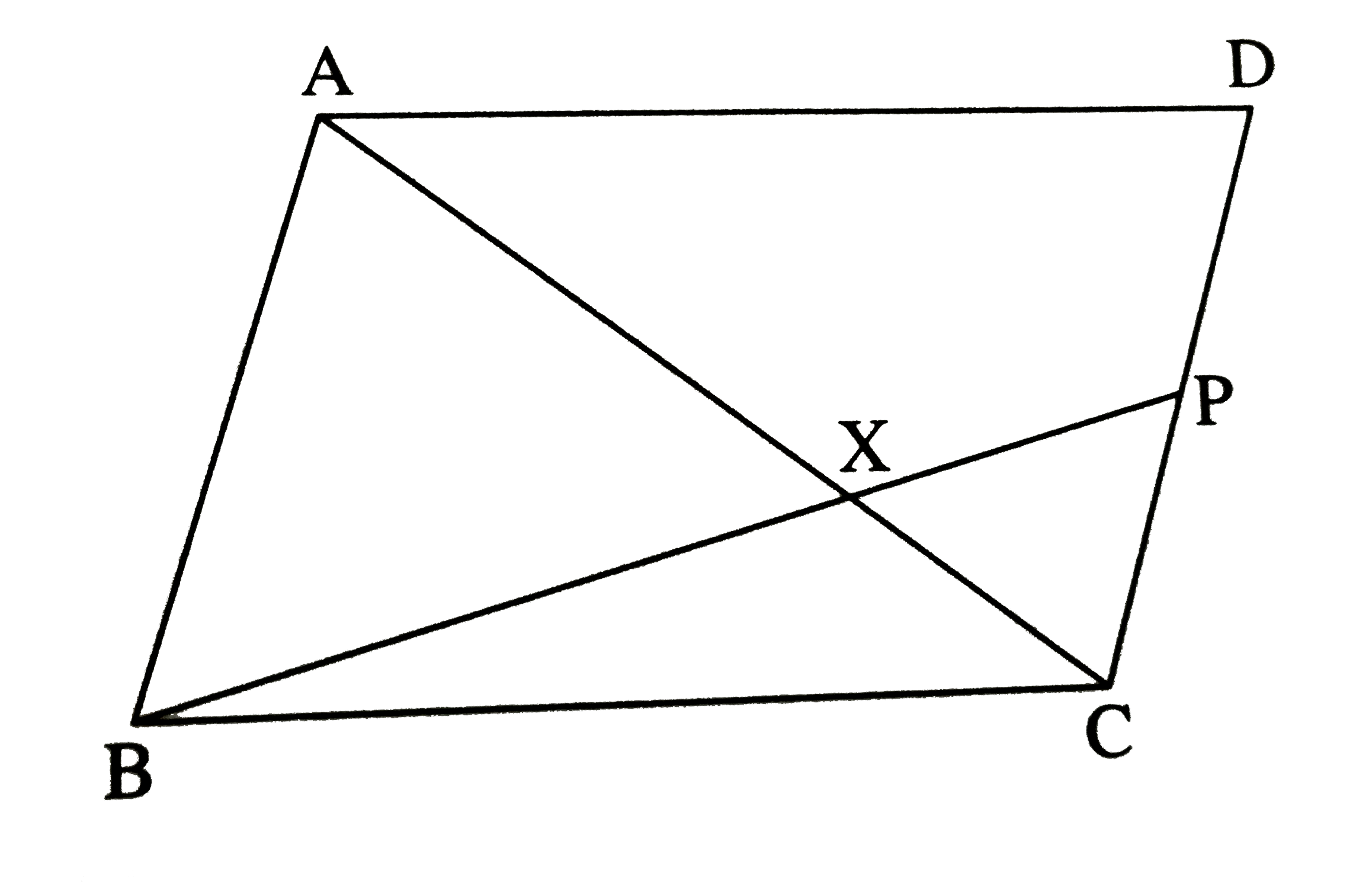
View SolutionBisector of ∠B and ∠C in ΔABC meet each other at P. Line AP cuts the sides BC at Q.
Prove: APPQ=AB+ACBC.
View Solutionसिद्ध कीजिए कि:
∣∣∣ad+bcbd−acac−bdad+bc∣∣∣=(a2+b2)(c2+d2).
View SolutionIn the figure seg AC and seg BD intersects each other at point P and APCP=BPDP . Then Prove that ΔABP~ΔCDP.
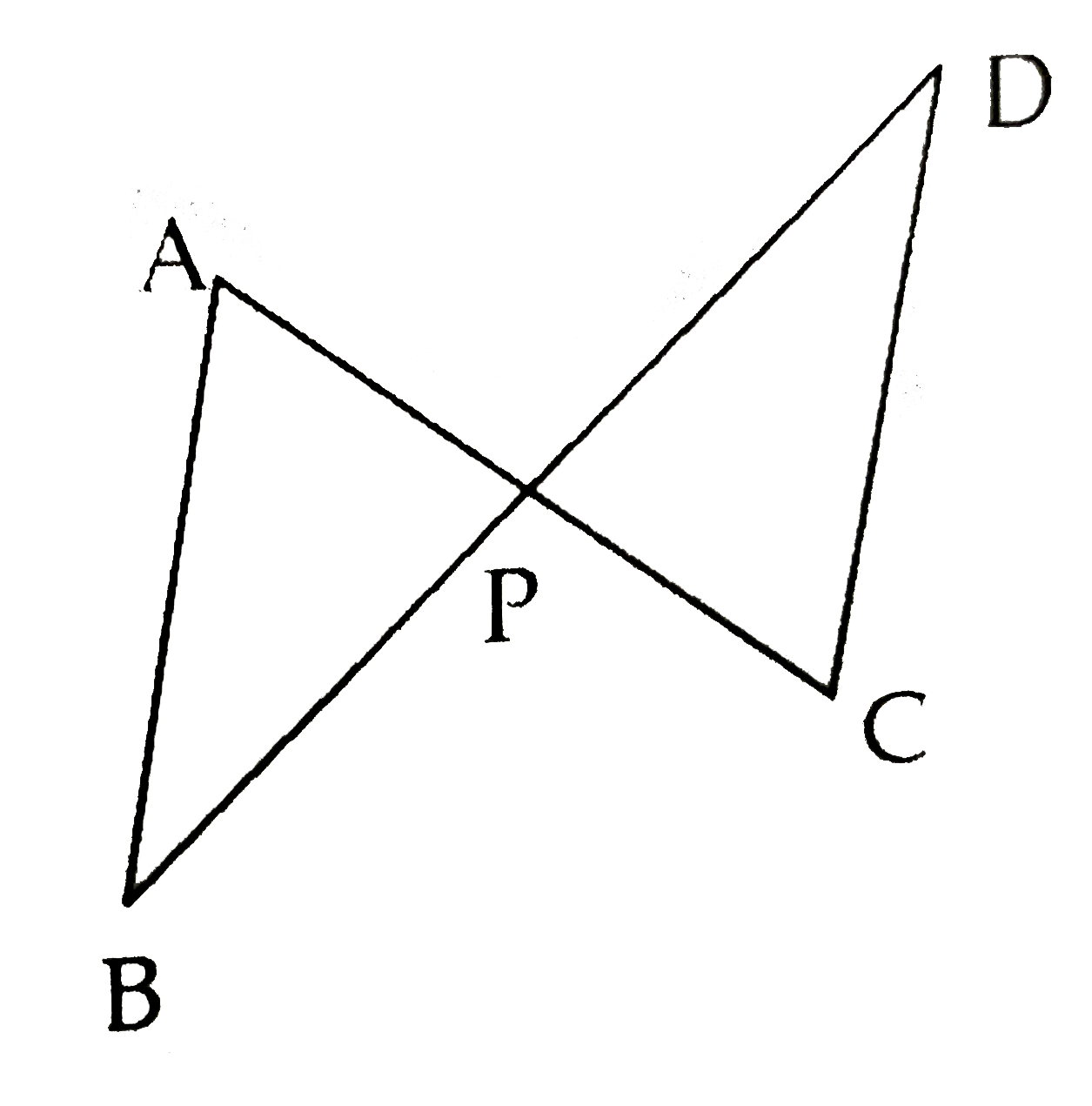
View SolutionIn □ABCD,seg AD∣∣seg BC. Diagonal AC and diagonal BC intersect each other in point P. Then show that APPD=PCBP
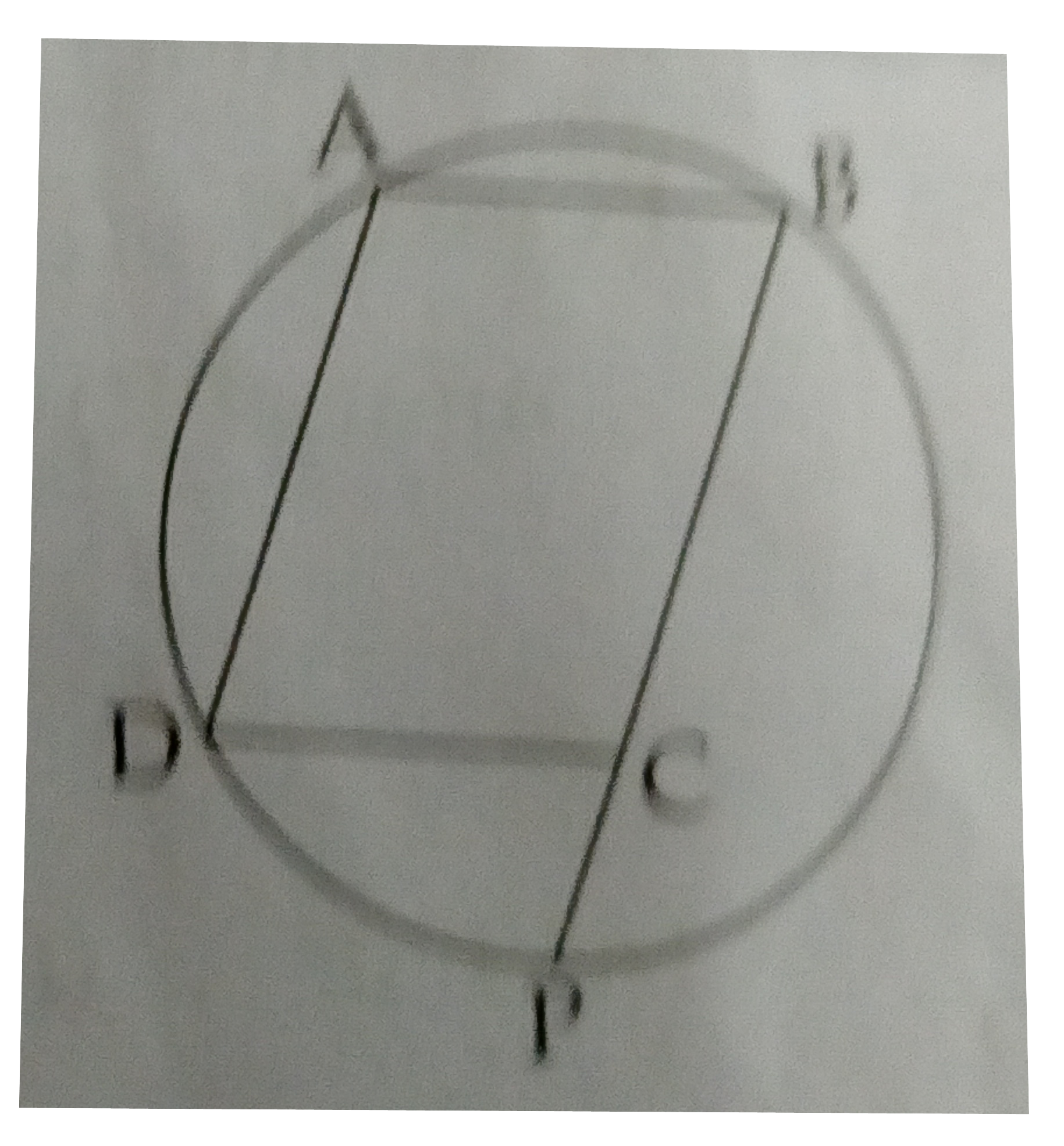
View Solution□ABCD is a parallelogram . Side BC intersects circle at point P . Prove that DC = DP .
View Solution
