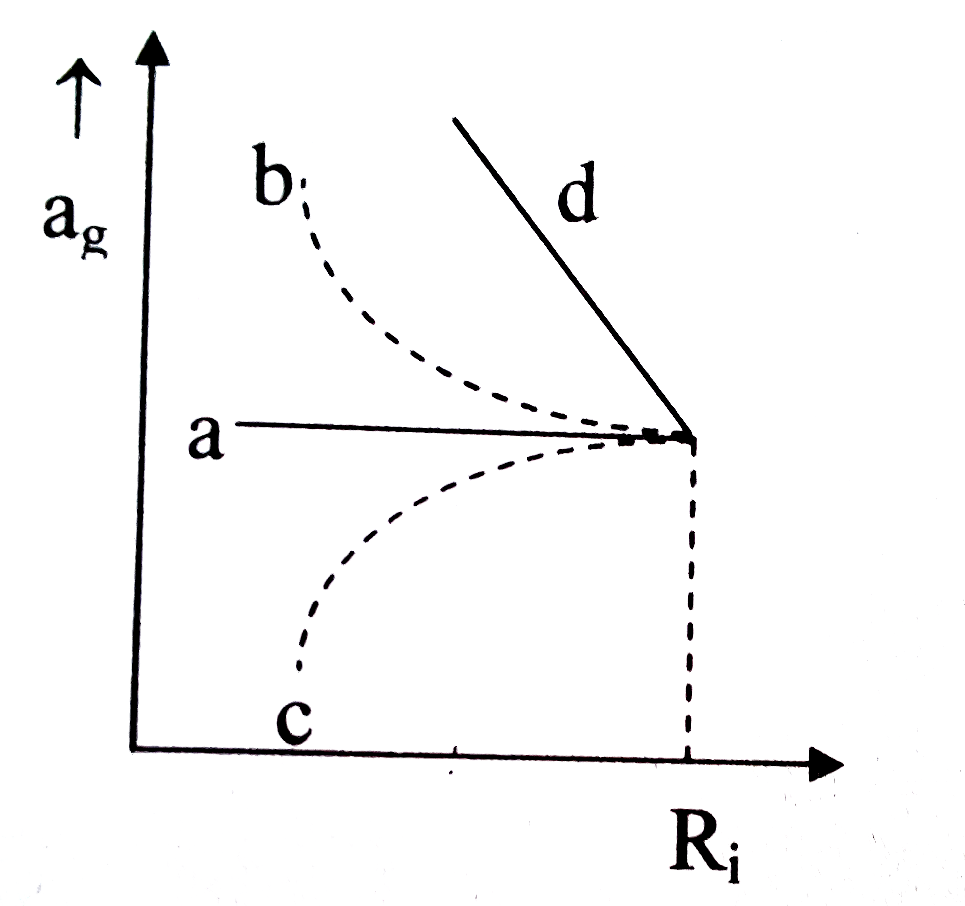
A (non-rotating) star collapses onto itself from an initial radius R, its mass remaining unchanged. Which curve in the figure best gives the gravitational acceleration ag on the surface of the star as a function of radius of star during collapse?
 Solution in Marathi
Solution in Marathi
a
b
c
d
The correct Answer is:B
Step by step video & image solution for A (non-rotating) star collapses onto itself from an initial radius R, its mass remaining unchanged. Which curve in the figure best gives the gravitational acceleration ag on the surface of the star as a function of radius of star during collapse? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A star of mass twice the solar mass and radius 10^(6) km rotates about its axis with an angular speed of 10^(-6)"rad"s^(-1) . What is the angular speed of the star when it collapses (due to inward gravitational) force) to a radius of 10^(4)km ?
View Solutionकथन : जब एक तारे का सिकुड़ते हुए पतन होता है तो इसका कोणीय वेग बढ़ता है।
कारण : तारे का द्रव्यमान कम होता जाता है।
View Solution(A) : The spin angular velocity of a star is greatly enhanced when it collapse under gravitiational pull and become a neuton star.
(R ) : According to law of conservation of angular momentum there is increase in angular velocity of collapsing star.
View SolutionWhat stops the collapse of a white dwarf and a neutron star ?
View SolutionAn impermeable star shrinks itself from the initial radius R in such a way that its mass remains fixed. Which of the given curves represents the gravitational acceleration on the star's surface as a function of the radius of the star?
View SolutionThe angular velocity of rotation of star (of mass M and radius R ) at which the matter start to escape from its equator will be
View SolutionThe mass ofa star is 3.98×1030 kg and its radius is 106 km. It rotates.about its axis with an angular speed of 10−6 rad/s. Calculate the speed of the star when it collapses to a radius of 104 km ? Assume the moment of inertia of the star to be 25mr2.
View Solution
