Two particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then Solution in Marathi
accelerations of both the particles are equal.
acceleration of the particle of mass m1 is proportional to m1.
acceleration of the particle of mass m1 is proportional to m2.
acceleration of the particle of mass m1 is inversely proportional to m1.
The correct Answer is:C
Step by step video & image solution for Two particles of mass m_(1) and m_(2), approach each other due to their mutual gravitational attraction only. Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (4.3 Law of conservation of momentum)23videos
FORCE
- BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (4.4 Elastic and inelastic collision)23videos
FORCE
- BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (4.0 Introduction)21videos
FORCE
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - EXCERCISE156videos
ELECTROSTATICS
- BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (EVALUATION TEST)21videos
FRICTION IS SOLIDS AND LIQUIDS
Similar Questions
An explosion blows a rock into three parts. Two parts go off at right angles to each other . These two are 1kg first part moving with a velocity of 12ms−1and2kg second part moving with a velocity of 8ms−1. If the third part flies off with a velocity of 4ms−1. Its mass would be
05:36View SolutionA bullet hits and gets embedded in a solid block resting on a frictionless surface. In this process, which of the following is correct ?
02:20View SolutionWhen a bus suddenly takes a turn, the passengers are thrown outwards because of
03:34View SolutionElectrostatic means study of
02:40View SolutionA body while sliding went straight down an incline of 45∘ to the horizontal and was subjected to a coefficient of kinetic friction of 0.20. Starting from rest, hwo long did it take him to reach a speed of 50km/hr? (Ignore air resistance and take h=10m/s2)
08:14View SolutionTwo particles of masses m_(1) and m_(2) initially at rest a infinite distance from each other, move under the action of mutual gravitational pull. Show that at any instant therir relative velocity of approach is sqrt(2G(m_(1)+m_(2))//R) where R is their separation at that instant.
04:30View SolutionTwo masses m_(1) and m_(2)(m_(1)ltm_(2)) are released from rest finite distance. They start under their mutual gravitational attraction-
03:34View SolutionTwo particles of mass m1andm2 are in space at separation →r [vector from m(1) to m2]. The only force that the two particles experience is the mutual gravitational pull. The force applied by m1onm2is→F. Prove that μd2→rdt2=→F where μm1m2m1+m2 is known as reduced mass for the two particle system .
 03:08View Solution
03:08View SolutionConsider a system of two particles of masses m1 and m2 separated by a distance r. Suppose they start to move towards each other due to their mutual attraction (attractive force may be electrical, gravitational, etc.).
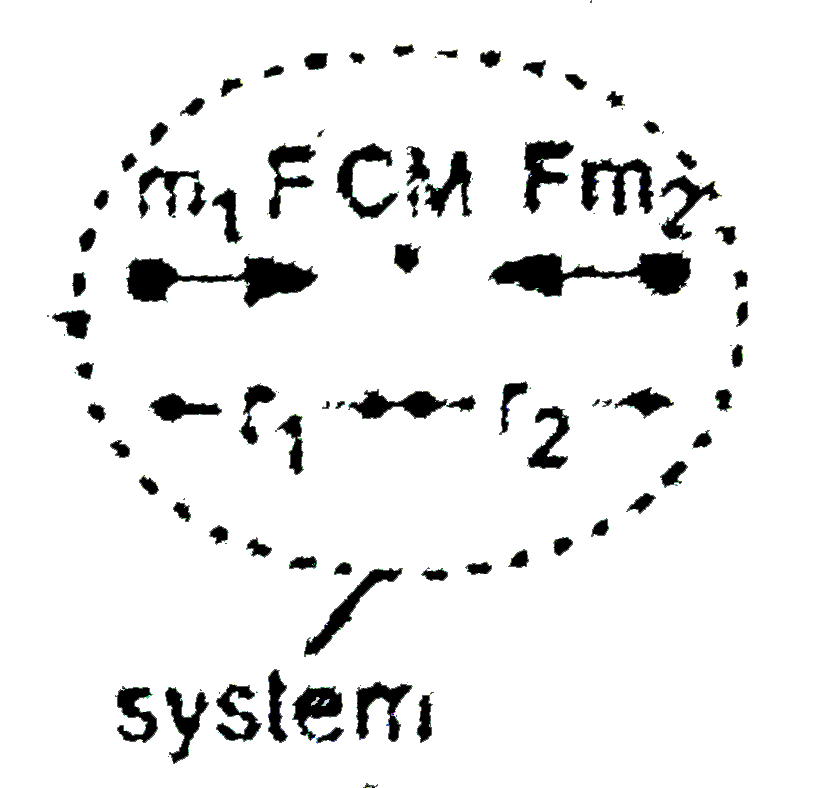 02:20View Solution
02:20View SolutionTwo particles m1 and m2 are initially at rest at infinite distance. Find their relative velocity of approach due to gravitational attraction when their separation is d.
05:22View SolutionTwo particles of mass m_(1) and m_(2) , approach each other due to their mutual gravitational attraction only. Then
04:05View SolutionTwo masses m1 and m2(m1<m2) are released from rest from a finite distance. They start under their mutual gravitational attraction
01:29View SolutionTwo particles of mass m_(1)andm_(2) , approach each other due to their mutual gravitational attraction only. Then:
View SolutionTwo particles of mass m1andm2, approach each other due to their mutual gravitational attraction only. Then:
06:00View SolutionTwo particle of mass m_1 and m_2 approach each other due to their mutual gravitational attraction only. Then
View SolutionTwo masses m_(1) and m_(2) are initially at rest at infinite distance. They approach each other due to gravitational attraction. What is the speed of approach at a distance r between them?
04:08View Solution

