What should be the minimum value of refractive index of a prism of refractive angle A, so that there is no emergent ray irrespective of angle of incidence?
sinA2
cosA2
cosecA2
secA2
The correct Answer is:C
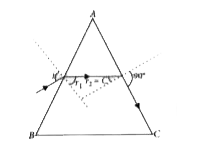
If the ray just emerges from face AC, e=90∘ and r2=C ….(i)
From Snell.s law at face AB, we have
1sini=nsinr1…(ii)
A=r1+r2=r1+C…(iii)
From eqn. (ii) n is minimum when r1 is maximum , i.e., r1=C. In this case i=90∘
From eqn. (iii) , A=2C or C=A/2
From eqn. (ii),
sin C=1n, sinA2=1n
∴ n=cosecA2
Topper's Solved these Questions
- MODEL TEST PAPER 1 BOOK - MTG-WBJEECHAPTER - MODEL TEST PAPER 1 EXERCISE - PHYSICS (Category) 3 : Single Option correct type (2 mark)
5 Videos
- MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONBOOK - MTG-WBJEECHAPTER - MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONEXERCISE - WB-JEE Previous years questions
17 Videos
Similar Questions
What should be the minimum value of refractive index of a prism, refracting angle A, so that there is no emergent ray irrespective of the angle of incidence?

View SolutionWhat should be the minimum value of refractive index of a prism, refracting angle A, so that there is no emergent ray irrespective of the angle of incidence?

View Solution
Knowledge Check
A ray of light suffers minimum deviation when incident on an equilateral prism of refractive index √2 . What is the angle of incidence ?
A30∘B45∘C60∘D90∘What is the angle of incidence for an equilateral prism of refractive index √3 so that the ray si parallel to the base inside the prism?
A30∘B45∘C60∘DEither 30∘ or 60∘A prism of refractive index sqrt2 has refractive angle 60∘. In the order that a ray suffers minimum deviation it should be incident at an angle of
A45∘B90∘C30∘DNone
The refractive index of the material of a prism of refracting angle 45∘ is 1.6 for a certain monochromatic ray. What will be the minimum angle of incidence of this ray on the prism so that no TIR takes place as the ray comes out of the prism.
View SolutionThe refractive index of the material of a prism of refracting angle 45∘ is 1.6 for a certain monochromatic ray. What will be the minimum angle of incidence of this ray on the prism so that no TIR takes place as the ray comes out of the prism.
View SolutionA prism of refractive index √2 has refractive angle 60∘ . Find the angle of incidence so that a ray minimum deviation.
View SolutionWhat is the angle of incidence for an equilateral prism of refractive index √3 so that the ray si parallel to the base inside the prism?
View SolutionA prism of refractive index sqrt2 has refractive angle 60∘. In the order that a ray suffers minimum deviation it should be incident at an angle of
View Solution
