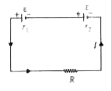
Two cells of same emf epsilon but of different internal resistances r

Two cells of the same e.mf. e but different internal resistances $r_{1} and r_{2}$ are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

A $r_{1} - r_{2}$
B $\frac{r_{1}}{r_{2}}$
C $r_{1} r_{2}$
D $r_{1} + r_{2}$
Tow cells with the same emf E and different internal resistances $r_{1}$ and $r_{2}$ are connected in series to an external resistances R . The value of R so that the potential difference across the first cell be zero is
A $\sqrt{r_{1} r_{2}}$
B $r_{1} + r_{2}$
C $r_{1} - r_{2}$
D $\frac{r_{1} + r_{2}}{2}$
Thousand cells of same emf E and same internal resistance r are connected is series in same order without an external resistance . The potential drop across 399 cells is found to be .
AZero
B399E
C601E
D1000E

Two cells of same emf $ε$ but of different internal resistances $r_{1}$ and $r_{2}$ are connected in series with an external resistance R. The potential drop across the first cell is found to be zero. The external resistance R is