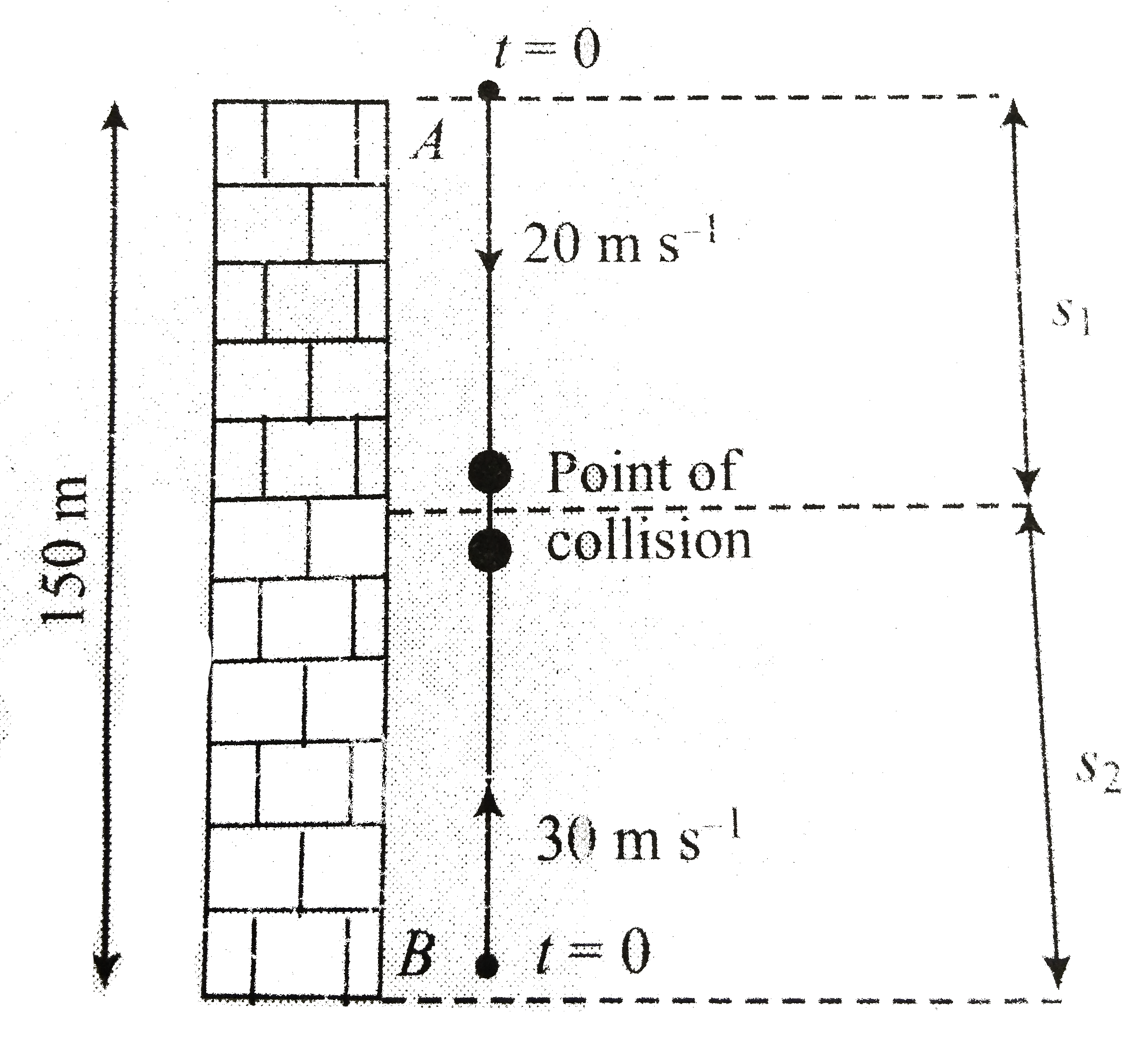
A ball is thrown downwards with a speed of $20 m / s$ from top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of $30 m / s$ from the foot of the building . Find the time when both the balls will meet . $(g = 10 m / s^{2})$

Text Solution

Verified by Experts

(i) $S_{1} = 20 t + 5 t^{2} + S_{2} = 30 t - 5 t^{2}$
$150 = 50 t$
$t = 3 s$ .

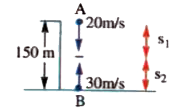
(ii)Relative acceleration of both is zero since both have acceleration in downward direction.
${\vec{a}}_{A B} = {\vec{a}}_{A} - {\vec{a}}_{B} = g - g = 0$
${\vec{V}}_{B A} = 30 - (- 20) = 50$
$S_{B A} = V_{B A} \times t$
$t = \frac{S_{B A}}{V_{B A}} = \frac{150}{50} = 3 s$

Updated on:21/07/2023

A ball is dropped from the top of a building of height 80 m. At same instant another ball is thrown upwards with speed 50 m/s from the bottom of the building. The time at which balls will meet is
A1.6 s
B5 s
C8 s
D10 s
A ball is dropped from the top of a building 100 m high. At the same instant another ball is thrown upwards with a velocity of $40 m s^{- 1}$ form the bottom of the building. The two balls will meet after.
A5 s
B2.5 s
C2 s
D3 s