The masses of the earth and moon are M and M/n respectively. Their centres are separated by a distance 2r. The minimum speed with whicih a particle of mass m should be projected from a point midway the two centres so as to escape to infinity is
√GM(n+1)nr
√2GM(n+1)nr
√GM(n+1)2nr
√2(GMn)(n+1)r
The correct Answer is:B
Topper's Solved these Questions
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - LECTURE SHEET (EXERCISE -III ) Orbital velocity & escape velocity (More than One correct answer Type Questions )
6 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - LECTURE SHEET (EXERCISE -III ) Orbital Objective & escape velocity (Linked Comprehension Type Questions )
2 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - LECTURE SHEET (EXERCISE -II ) Relation between g & G and variation of g (Linked Comprehension Type Questions )
3 Videos
- GAUSS.S LAW BOOK - AAKASH SERIESCHAPTER - GAUSS.S LAW EXERCISE - PROBLEMS (LEVEL - II)
12 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
Similar Questions
The masses and radii of the Earth and the Moon are M1,R1andM2,R2 respectively. Their centres are at a distance d apart. The minimum speed with which a particle of mass m should be projected from a point midway between the two centres so as to escape to infinity is ........
View SolutionThe masses and radii of the Earth and the Moon are M1,R1andM2,R2 respectively. Their centres are at a distance d apart. The minimum speed with which a particel of mass m should be projected from a point midway between the two centres so as to escape to infinity is ........
View Solution
Knowledge Check
The radii of a planet and its satellite are 2r and r and their densities are ρ and 2ρ respectively. Their centres are separated by a distance d. The minimum speed with which a body should be projected from the mid point of the line joining their centres so that the body escapes to infinity is (G-universal gravitational constant)
A4⎡⎣√10Gπr3ρ3d⎤⎦B√40Gπr3ρ3d⎤⎦C2⎡⎣√10Gπr3ρd⎤⎦D14⎡⎣√10Gπr3ρ3d⎤⎦Two point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)Two point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)
The masses and radii of the earth an moon are M1andR1andM2,R2 respectively. Their centres are at a distacne r apart. Find the minimum speed with which the particle of mass m should be projected from a point mid-way between the two centres so as to escape to infinity.
View SolutionThe masses and radii of the earth an moon are M1andR1andM2,R2 respectively. Their centres are at a distacne d apart. Find the minimum speed with which the particle of mass m should be projected from a point mid-way between the two centres so as to escape to infinity.
View SolutionThe masses and radii of the earth and moon are (M1,R1) and (M2,R2) respectively. Their centres are at a distance r apart. Find the minimum escape velocity for a particle of mass 'm' to be projected from the middle of these two masses :
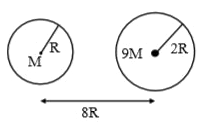
View SolutionSuppose two planets (spherical in shape) of radii R and 2R, but mass M and 9 M respectively have a centre to centre separation 8 R as shown in the figure. A satellite of mass 'm' is projected from the surface of the planet of mass 'M' directly towards the centre of the second planet. The minimum speed 'v' required for the satellite to reach the surface of the second planet is √a7GMR then the value of 'a' is ________.
[Given : The two planets are fixed in their position]
View SolutionTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View Solution
