The masses and radii of the Earth and the Moon are M1,R1andM2,R2 respectively. Their centres are at a distance d apart. The minimum speed with which a particle of mass m should be projected from a point midway between the two centres so as to escape to infinity is ........
The correct Answer is:NA
To solve the problem of finding the minimum speed with which a particle of mass m should be projected from a point midway between the Earth and the Moon so as to escape to infinity, we can use the principle of conservation of mechanical energy.
1. Identify the Initial Conditions:
- The particle is projected from the midpoint between the Earth and the Moon. The distance between the centers of the Earth and Moon is d.
- Therefore, the distance from the midpoint to the center of the Earth is d2 and the same applies to the distance to the center of the Moon.
2. Calculate the Initial Potential Energy:
- The gravitational potential energy U between two masses M and m separated by a distance r is given by:
U=−GMmr
- For the particle at the midpoint, the potential energy due to the Earth is:
U1=−GM1md2=−2GM1md
- The potential energy due to the Moon is:
U2=−GM2md2=−2GM2md
- Therefore, the total initial potential energy Ui is:
Ui=U1+U2=−2GM1md−2GM2md=−2G(M1+M2)md
3. Final Conditions at Infinity:
- At infinity, the potential energy Uf is zero, and we assume the kinetic energy Kf is also zero for the minimum speed case (the particle just escapes).
- Thus, the total mechanical energy at infinity is:
Ef=Kf+Uf=0+0=0
4. Apply Conservation of Mechanical Energy:
- According to the conservation of mechanical energy:
Ei=Ef
- Therefore:
Ki+Ui=0
- The initial kinetic energy Ki is given by:
Ki=12mv20
- Substituting the initial potential energy:
12mv20−2G(M1+M2)md=0
5. Solve for Minimum Speed v0:
- Rearranging the equation gives:
12mv20=2G(M1+M2)md
- Dividing both sides by m (assuming m≠0):
12v20=2G(M1+M2)d
- Multiplying both sides by 2:
v20=4G(M1+M2)d
- Taking the square root:
v0=√4G(M1+M2)d=2√G(M1+M2)√d
Final Answer:
The minimum speed with which a particle of mass m should be projected from the midpoint between the Earth and the Moon to escape to infinity is:
v0=2√G(M1+M2)√d
- The particle is projected from the midpoint between the Earth and the Moon. The distance between the centers of the Earth and Moon is d.
- Therefore, the distance from the midpoint to the center of the Earth is d2 and the same applies to the distance to the center of the Moon.
- The gravitational potential energy U between two masses M and m separated by a distance r is given by:
U=−GMmr
- For the particle at the midpoint, the potential energy due to the Earth is:
U1=−GM1md2=−2GM1md
- The potential energy due to the Moon is:
U2=−GM2md2=−2GM2md
- Therefore, the total initial potential energy Ui is:
Ui=U1+U2=−2GM1md−2GM2md=−2G(M1+M2)md
- At infinity, the potential energy Uf is zero, and we assume the kinetic energy Kf is also zero for the minimum speed case (the particle just escapes).
- Thus, the total mechanical energy at infinity is:
Ef=Kf+Uf=0+0=0
- According to the conservation of mechanical energy:
Ei=Ef
- Therefore:
Ki+Ui=0
- The initial kinetic energy Ki is given by:
Ki=12mv20
- Substituting the initial potential energy:
12mv20−2G(M1+M2)md=0
- Rearranging the equation gives:
12mv20=2G(M1+M2)md
- Dividing both sides by m (assuming m≠0):
12v20=2G(M1+M2)d
- Multiplying both sides by 2:
v20=4G(M1+M2)d
- Taking the square root:
v0=√4G(M1+M2)d=2√G(M1+M2)√d
The minimum speed with which a particle of mass m should be projected from the midpoint between the Earth and the Moon to escape to infinity is:
v0=2√G(M1+M2)√d
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - True/False1videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - SCQ_TYPE12videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Integer5videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
Similar Questions
The masses and radii of the earth an moon are M1andR1andM2,R2 respectively. Their centres are at a distacne d apart. Find the minimum speed with which the particle of mass m should be projected from a point mid-way between the two centres so as to escape to infinity.
View SolutionTwo particles, each of mass m, are a distance d apart. To bring a third particle, also having mass m, from far away to the point midway between the two particles an external agent does work given by:
View Solution
Knowledge Check
- Question 1 - Select One
Two spheres of masses 2 M and M are intially at rest at a distance R apart. Due to mutual force of attraction, they approach each other. When they are at separation R/2, the acceleration of the centre of mass of sphere would be
A0m/s2Bgm/s2C3gm/s2D12gm/s2
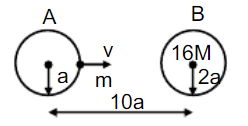
Two planets of mass M and 16M of radius a and 2a respectively, are at distance 10a. Find minimum speed of a particle of mass m at surface of smaller planet so that it can reached from smaller planet to larger planet.View SolutionTwo bodies of mass M and 4M kept at a distance y apart. Where should a small particle of mass m be placed from M so that the net gravitational force on it is zero
View SolutionIf d is the distance between the centre of the earth of mass M1 and the moon of mass M2, then the velocity with which a body should be projected from the mid point of the line joining the earth and the moon, so that it just escape is
View SolutionThe minimum and maximum distance of a satellite from the centre of the earth are 2R and 4R respectively, where R is the radius of earth and M is the mass of the earth. The radius of curvature at the point of maximum distance is
View SolutionConsider a two particle system with the particles having masses m1andm2. If the first particles pushed towards the centre of mass through a distance d, by what distance should the second particle be moved so as the keep the centre of mass at the same position?
View SolutionTwo concentric shells have masses M and m and their radii are R and r, respectively, where R>r. What is the gravitational potential at their common centre?
View SolutionTwo planets have masses M and 16 M and their radii are a and 2a, respectively. The separation between the centres of the planets is 10a. A body of mass m is fired trom the surface of the larger planet towards the samller planet along the line joining their centres. For the body to be able to reach at the surface of smaller planet, the minimum firing speed needed is :
View Solution

