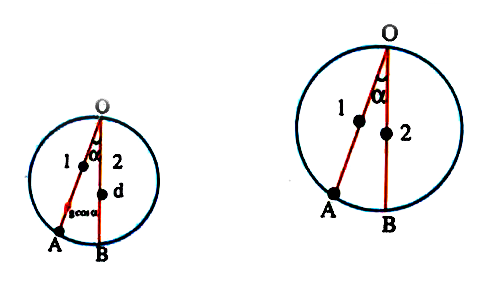
Two particles 1 and 2 are allowed to descend on the two frictionless chord OA and OB of a vetical circle , at the same instant from point O. The ratio of the velocities of the particles 1 and 2 respectively , when they reach on the circumference will be (OB is the diameter)

Text Solution

Verified by Experts

$O A = d {cos α}_{O A} = g cos α$
Along OA $\Rightarrow V_{A}^{2} = 2 g cos α . D cos α$
Along OB
$V_{B}^{2} = 2 g d \Rightarrow \frac{V_{A}}{V_{B}} = cos α$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
$\begin{matrix} Column A & In the figure, two circle with centers A and B touch a larger circle with center O internally. The ratio of the radii of Circle A to Circle B is 7 : 9 & Column B O A & O B \end{matrix}$

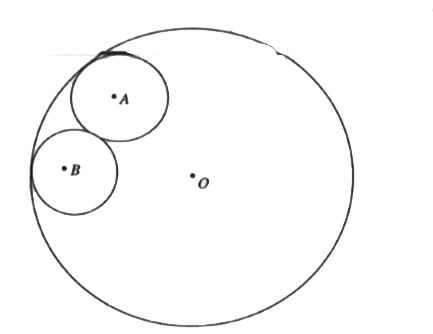AIf column A is larger
BIf column B is larger
CIf the columns are equal
DIf there is not enough information to decide
Question 2 - Select One
Two tangents OA and OB are drawn to the circle $x^{2} + y^{2} + 4 x + 6 y + 12 = 0$ from origin O. The circumradius of $Δ O A B$ is :
A $\frac{1}{2}$
B1
C2
D $\frac{\sqrt{13}}{2}$
Question 3 - Select One
Points A(a) and B (b) are on $x y = 1$ , Circles with OA and OB as diameter, where O is the origin are drawn to intersect at p , then OP intersects the curve at
A $(\frac{1}{\sqrt{a b}}, \sqrt{a b})$
B $(- \frac{1}{\sqrt{a b}}, - \sqrt{a b})$
C $(\sqrt{a b}, \frac{1}{\sqrt{a b}})$
Dall of these

AAKASH SERIES-MOTION IN A STRAIGHT LINE-PROBLEM

Home
Ask Doubt
Profile