An ideal gas expands isothermally from a volume $V_{1} to V_{2}$ and then compressef to original volume $V_{1}$ adiabatically. Initial pressure is $P_{1}$ and final pressure is $P_{3}$ . The total work done is W. Then what is its value and its conditions.

Text Solution

Verified by Experts

Slope of adiabatic process at a given state (P,V,T) is more than the slope of isothermal process. The corresponding $P - V$ graph for the two processes is as shown in figure.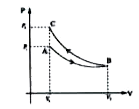
In the graph, A,B is isothermal and BC is adiabatic. $W_{A B}$ = positive (as volume is increasing) plus, $| W_{B C} | > | W_{A B} |$ , as area under P-V graph gives the work done.
Hence, $W_{A B} + W_{B C} = W < 0$
From the graph itself, it is clear that $P_{3} > P_{1}$

Updated on:21/07/2023

An ideal gas expands isothermally from volume $V_{1}$ to $V_{2}$ and is then compressed to original volume $V_{1}$ adiabatically. Initialy pressure is $P_{1}$ and final pressure is $P_{3}$ . The total work done is $W$ . Then
A $P_{3} > P_{1}, W > 0$
B $P_{3} < P_{1}, W < 0$
C $P_{3} > P_{1}, W < 0$
D $P_{3} = P_{1}, W = 0$
An ideal gas expands isothermally from volume $V_{1}$ to $V_{2}$ and is then compressed to original volume $V_{1}$ adiabatically. Initialy pressure is $P_{1}$ and final pressure is $P_{3}$ . The total work done is $W$ . Then
A $P_{3} > P_{1}, W > 0$
B $P_{3} < P_{1}, W < 0$
C $P_{3} > P_{1}, W < 0$
D $P_{3} = P_{1}, W = 0$
A sample of ideal gas undergoes isothermal expansion in a reversible manner from volume $V_{1}$ to volume $V_{2}$ . The initial pressure is $P_{1}$ and the final pressure is $P_{2}$ . The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume $V_{1} \to V_{2}$ . The initial pressure being same but final pressure is $P_{2}$ .
The work of expansion in adiabatic process $(w_{a d i})$ is related to work of expansion in isothermal process $(w_{i s o})$ is
A $w_{a d i} = w_{i s o}$
B $w_{a d i} < w_{i s o}$
C $w_{a d i} = 2 w_{i s o}$
D $w_{a d i} > w_{i s o}$