Let f:R→R be a differentiable function ∀ξnR . If the tangent drawn to the curve at any point ξn(a,b) always lies below the curve , thenSolution in Telugu
f'(x)>0,f''(x)<0∀x∈(a,b)
f(x)<0,f''(x)<0∀x∈(a,b)
f'(x)>0,f''(x)<0∀x∈(a,b)
f(x)≤0,f''(x)≤0∀x∈(a,b)
The correct Answer is:C
Step by step video & text solution for Let f:RtoR be a differentiable function AAxinR . If the tangent drawn to the curve at any point xin(a,b) always lies below the curve , then by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)10videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MATRIX MATCHING TYPE QUESTIONS)2videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - PRACTICE SHEET (EXERCISE -II) (LEVEL -II)(INTEGER TYPE QUESTIONS)4videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III35videos
MAXIMA & MINIMA
- BOOK - AAKASH SERIESCHAPTER - MEAN VALUE THEOREMSEXERCISE - PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )2videos
MEAN VALUE THEOREMS
Similar Questions
Let f(x)=(x−1)4(x−2)n, n in N.. Then f(x) has
02:41View SolutionThe function f(x)=√(ax3+bx2+cx+d) has its nonzero local minimum an d maximum values at x=-2 andx=2 , repectively . If a is a root of x2−x−x6=0 , then match the following
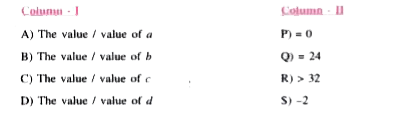 07:17View Solution
07:17View SolutionA right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter . If the maximum area of the triangle is M , then the value of 32√3Mc is _______
05:23View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
03:10View SolutionGiven f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )06:35View SolutionLet f:R→ be a differentiable function ∀x∈R . If the tangent drawn to the curve at any point x∈(a,b) always lies below the curve, then (a) f′(x)<0,fx<0∀x∈(a,b) (b)f′(x)>0,fx>0∀x∈(a,b) (c)f′(x)>0,fx>0∀x∈(a,b) (d)noneofthese
02:55View SolutionA curve is such that the mid-point of the portion of the tangent intercepted between the point where the tangent is drawn and the point where the tangent meets the y-axis lies on the line y=x. If the curve passes through (1,0), then the curve is
View SolutionA curve C has the property that if the tangent drawn at any point P on C meets the co-ordinate axis at A and B , then P is the mid-point of AB. The curve passes through the point (1,1). Determine the equation of the curve.
09:30View SolutionA curve is such that the length of the polar radius of any point on the curve is equal to the length of the tangent drawn at this point.Form the differential equation and solve it to find the equation of the curve.
01:14View SolutionTangent drawn at any point P on a curve meets x -axis at Q such that circumcentre of Delta POQ has abscissa half that of ordinate.The differential equation to such a curve is
03:51View SolutionThe sum of the squares of the perpendicular drawn from the points (0,1) and (0,−1) to any tangent to a curve is 2. The equation of the curve, is
05:25View Solutionमूलबिंदु की वक्र y=sinx पर खींची गयी स्पर्शियो के स्पर्श बिन्दु का बिन्दुपथ है-
01:38View SolutionThe normal at any point to a curve always passes through a given point (a, b) , if the curve passes through the origin, then the curve is a/an -
03:20View Solutionকোনো বক্রের যে-কোনো বিন্দুতে অভিলম্ব সর্বদা একটি প্রদত্ত বিন্দু (a,b) দিয়ে যায়, যদি বক্রটি মূলবিন্দুগামী হয়, তবে বক্রটি হয় একটি
02:50View SolutionLet f:R→ be a differentiable function ∀x∈R . If the tangent drawn to the curve at any point x∈(a,b) always lies below the curve, then (a) f′(x)<0,fx<0∀x∈(a,b) (b)f′(x)>0,fx>0∀x∈(a,b) (c)f′(x)>0,fx>0∀x∈(a,b) (d)noneofthese
05:22View Solution

