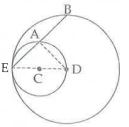
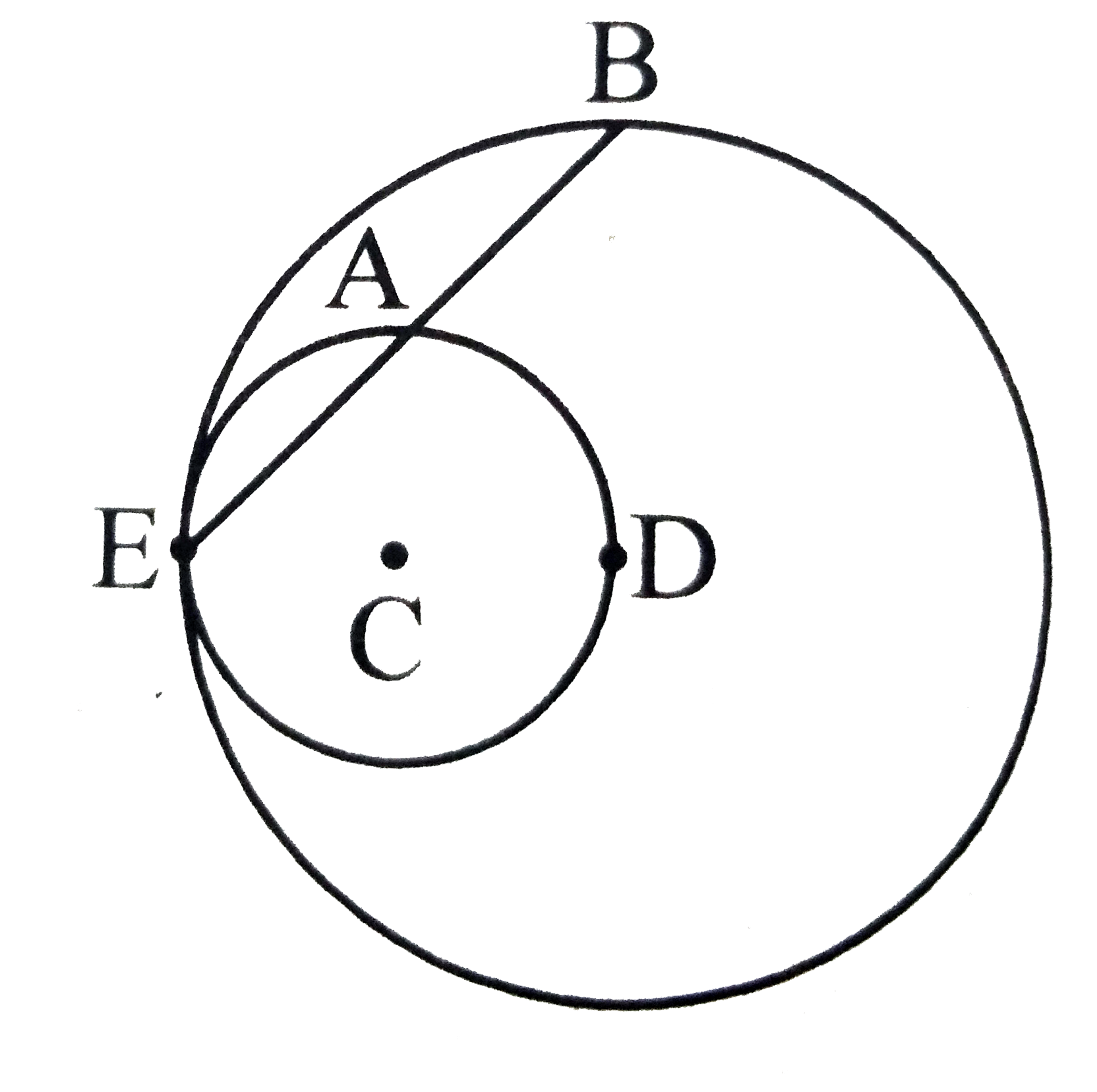
A circle with centre C touches the circle with centre D internally in the point E. Point D lies on the smaller circle. Chord EB of the external circle intersects internal circle at point A. Prove that segEA≅segAB
 Solution in Marathi
Solution in Marathi
Step by step video & image solution for A circle with centre C touches the circle with centre D internally in the point E. Point D lies on the smaller circle. Chord EB of the external circle intersects internal circle at point A. Prove that seg EA~=seg AB by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two circles of radii 5.5 cm and 3.3 cm respectively touch each other.What is the distance between their centres?
View SolutionRewrite the following statement in 'if-then' form. 'Diagonals of a parallelogram bisect each other.'
View SolutionSeg AB is parallel to Y-axis and co-ordinates of point A are (1,3), then co-ordinates of point B can be……….a) (3,1) b) (5,3) c) (3,0) d) (1,-3)
View SolutionIn the given figure (not to scale), O is the centre of the circle. A,B,C and D are concyclic and AB=CD . If /_MON =120^(@) , then find /_ OPN .
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the given figure, AB is a diameter, O is the center of the circle and ∠OCB=50∘ then find ∠DBC.
View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD ∣∣ chord AC.
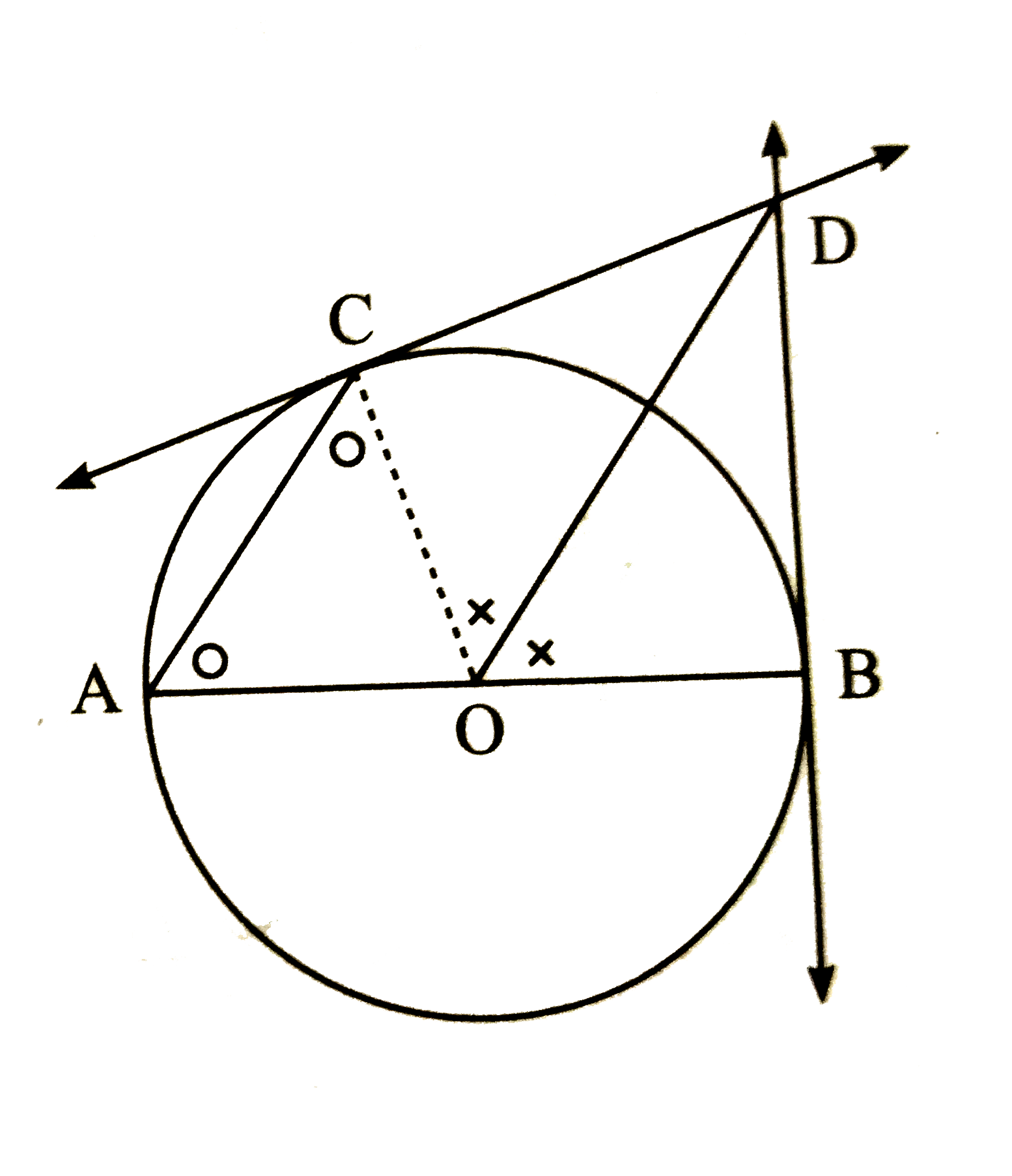
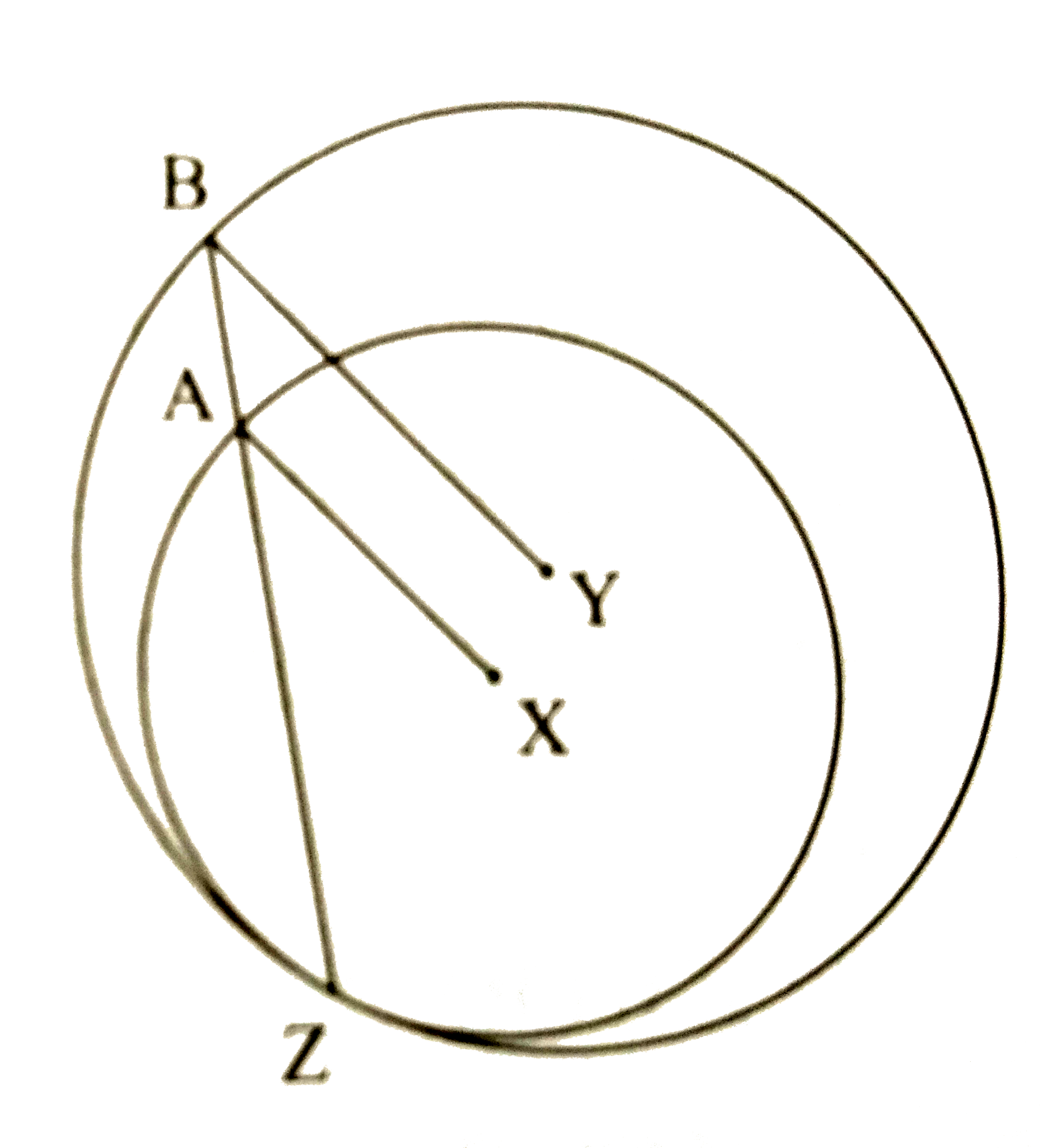
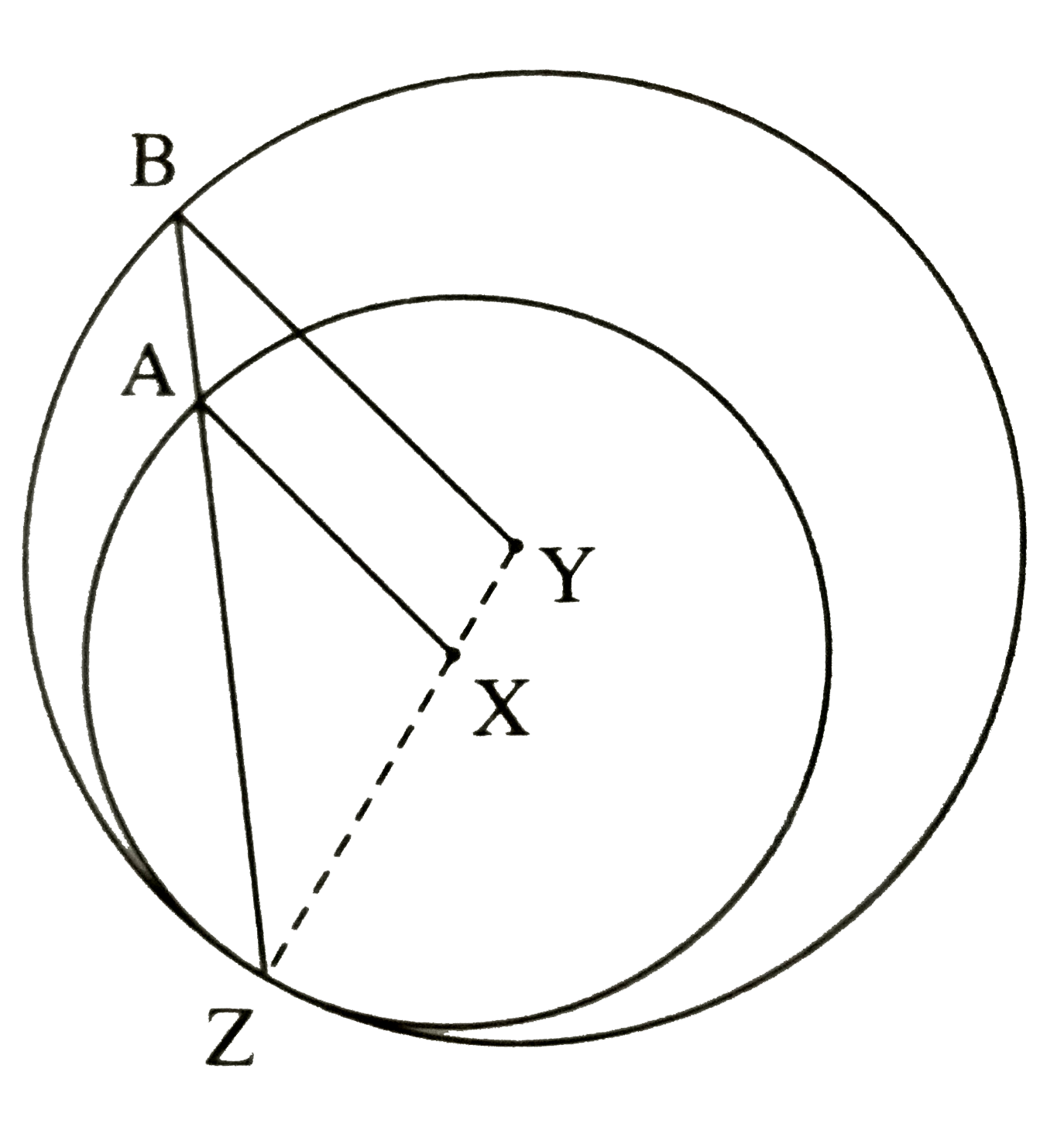
View SolutionIn the figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smaller circlea t point A. Prove that , seg AX ∣∣ seg BY
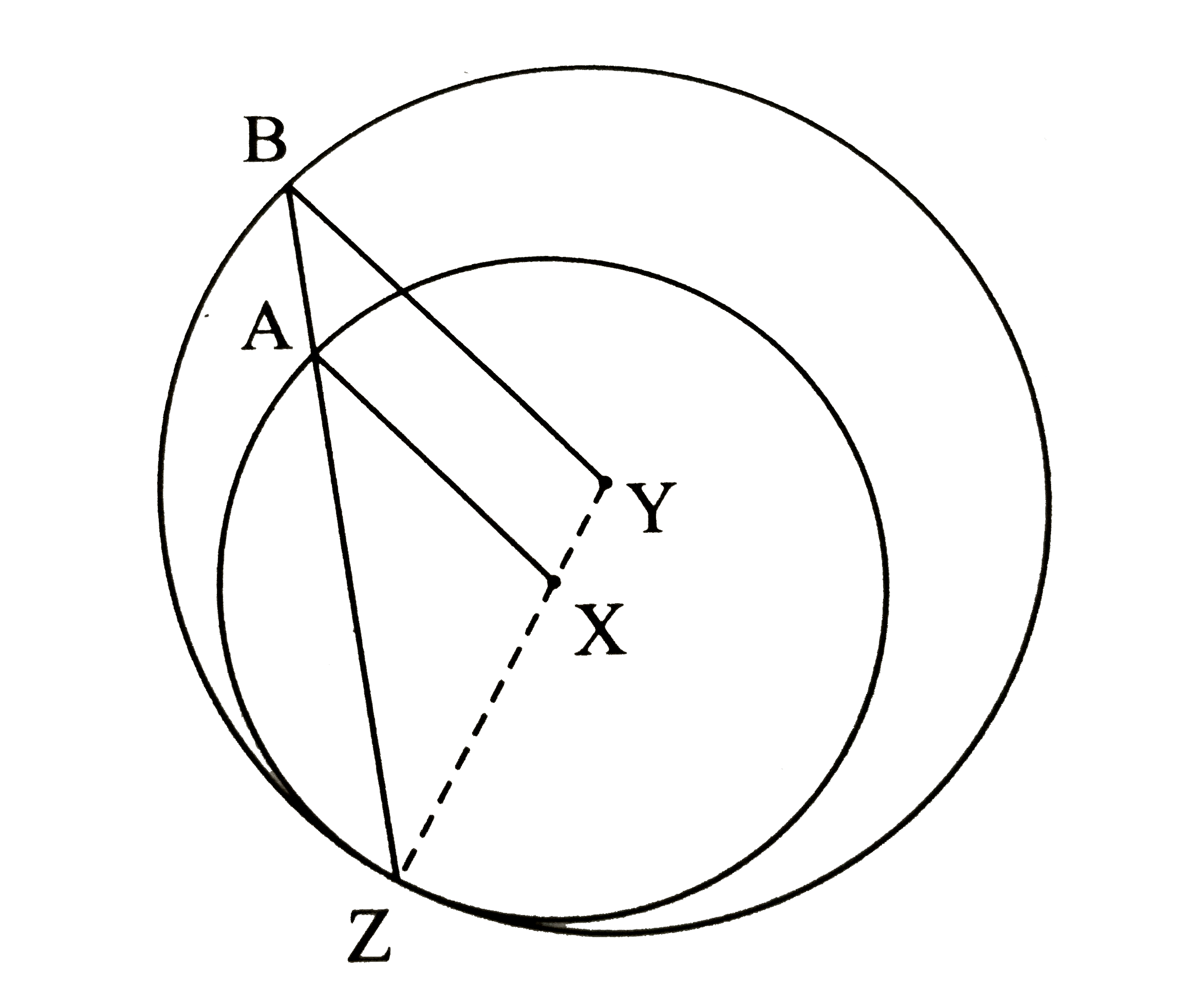
View SolutionIn the figure , circles with centres X and Y touch internally at point Z. Seg BZ is the chord of bigger circle and it intersects smaller k circle at point A.
Prove that seg AX∣∣ seg BY.
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.

View SolutionTwo circles with centres A and B touch each other internally. Another circle touches the larger circle internally at the point X and the smaller circle externally at the point Y. If O be the centre of that circle, prove that (OA + BO) is constant.
View SolutionIn the adjoining figure , circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the other circle intersects innet circle at point A. Prove that, seg EA≅seg AB.
View SolutionIn the figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smaller circle at point A. Prove that, seg AX || seg BY.
View SolutionIn figure, circles with centers C and D touch internally at point E. D lies on the inner circle. Chrd EB of the outer circle intersects inner circle at point A. Prove that, seg EA ≅ seg AB.

View SolutionIn figure, seg AB is a diameter of a circle with centre O. The bisector of ∠ACB intersects the circle at point D. Prove that seg AD ≅ seg BD. Complete the following proof by filling in the blanks

View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
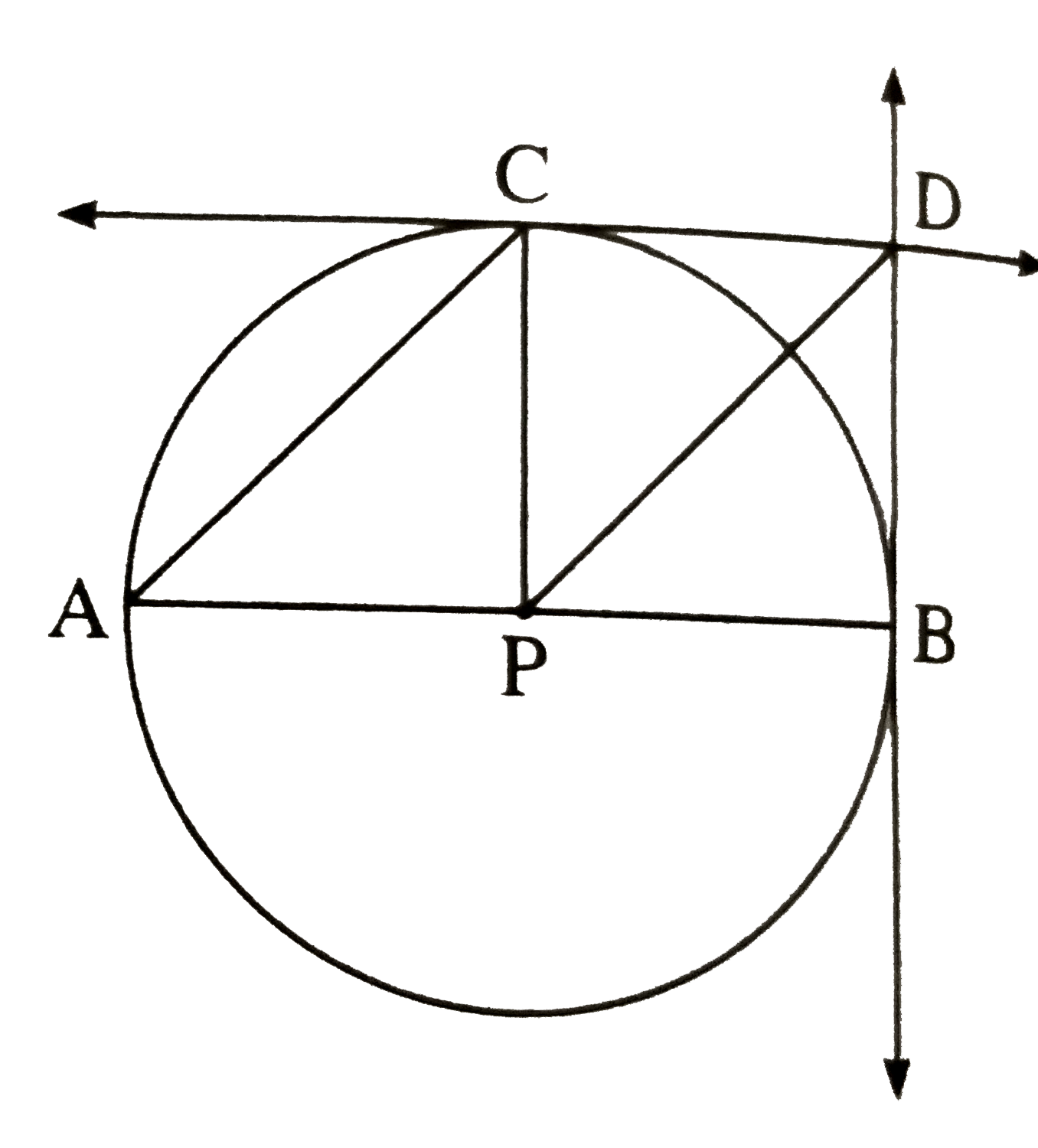
View Solution
